求过点P(-5,-4)且满足下列条件的直线方程:
(1)和直线x-3y+4=0垂直;
(2)倾斜角等于直线x-3y+4=0的倾斜角的二倍.
【答案】
分析:(1)设和直线x-3y+4=0垂直的直线方程为 3x+y+c=0,把点P(-5,-4)代入可得c=19,从而得到所求直线方程.
(2)由题意得直线x-3y+4=0的斜率
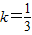
,设其倾斜角为α,则 tanα=

,且所求直线l
1的倾斜角为2α,故所求直线的斜率为 tan2α,由二倍角的正切公式求得tan2α 的值,
用点斜式求直线方程,并化为一般式.
解答:解:(1)设和直线x-3y+4=0垂直的直线方程为 3x+y+c=0,把点P(-5,-4)代入可得-15-4+c=0,故 c=19,
故所求直线方程为 3x+y+19=0.
(2)由题意得直线x-3y+4=0的斜率
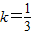
,设其倾斜角为α,则 tanα=

,且所求直线l
1的倾斜角为2α,
故所求直线的斜率为 tan2α=
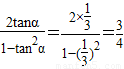
,
则所求直线方程为
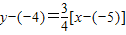
,即3x-4y-1=0.
点评:本题主要考查用点斜式求直线方程,用待定系数法求直线的方程,两直线平行、垂直的性质,二倍角的正切公式的应用,属于基础题.

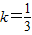 ,设其倾斜角为α,则 tanα=
,设其倾斜角为α,则 tanα= ,且所求直线l1的倾斜角为2α,故所求直线的斜率为 tan2α,由二倍角的正切公式求得tan2α 的值,
,且所求直线l1的倾斜角为2α,故所求直线的斜率为 tan2α,由二倍角的正切公式求得tan2α 的值,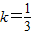 ,设其倾斜角为α,则 tanα=
,设其倾斜角为α,则 tanα= ,且所求直线l1的倾斜角为2α,
,且所求直线l1的倾斜角为2α,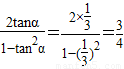 ,
,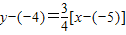 ,即3x-4y-1=0.
,即3x-4y-1=0.
