
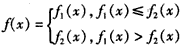 ,
,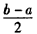 (闭区间[m,n]的长度定义为n-m)。
(闭区间[m,n]的长度定义为n-m)。 解:(Ⅰ)由f(x)的定义可知,f(x)=f1(x)(对所有实数x)等价于f1(x)≤f2(x)(对所有实数x),
这又等价于3|x-p1|≤2·3|x-p2|,即3|x-p1|-|x-p2|≤2对所有实数x均成立,(*)
易知函数|x-p1|-|x-p2|(x∈R)的最大值为|p2-p1| ,
故(*)等价于3|p2-p1|≤2,即|p2-p1|≤log32,这就是所求的充分必要条件.
(Ⅱ)分两种情形讨论.
(ⅰ)当|p1-p2|≤log32时,由(Ⅰ)知f(x)=f1(x)(对所有实数x∈[a,b]),
则由f(a)=f(b)及a<p1<b易知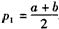 ,
,
再由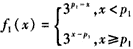 的单调性可知,
的单调性可知,
f(x)在区间[a,b]上的单调增区间的长度为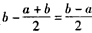 ,如下图,
,如下图, 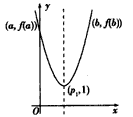
(ⅱ)当|p1-p2|>log32时,不妨设p1<p2,则p2-p1>log32,
于是,当x≤p1时,有f1(x)=3p1-x<3p2-x<f2(x),从而f(x)=f1(x);
当x≥p2时,f1(x)=3x-p1=3p2-p1·3x-p2>3log32·3x-p2=f2(x),从而f(x)=f2(x);
当p1<x<p2时,f1(x)=3x-p1及f2(x)=2·3p2-x,
由方程3x0-p1=2·3p2-x0,
解得f1(x)与f2(x)图象交点的横坐标为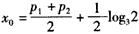 ,①
,①
显然 ,
,
这表明x0在p1与p2之间,
由①易知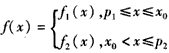 ;
;
综上可知,在区间[a,b]上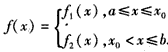 , 如下图所示,
, 如下图所示,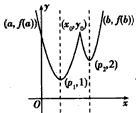
故由函数f1(x)与f2(x)的单调性可知,f(x)在区间[a,b]上的单调增区间的长度之和为(x0-p1)+(b-p2),由于f(a)=f(b),即3p1-a=2·3b-p2,得 p1+p2=a+b+log32,②
故由①、②得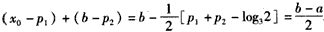 ;
;
综合(ⅰ)、(ⅱ)可知,f(x)在区间[a,b]上的单调增区间的长度之和为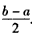 。
。


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| x |
| 4 |
| cosx |
| π |
| 2 |
| 8x |
| x2+1 |
| 9 |
| x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com