
(1)求椭圆方程;
(2)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,且线段MN的垂直平分线过定点G(![]() ,0),求k的取值范围.
,0),求k的取值范围.
解:(1)由题意椭圆的离心率e=![]() .∴
.∴![]() =
=![]() .∴a=2c.∴b2=a2-c2=3c2.
.∴a=2c.∴b2=a2-c2=3c2.
∴椭圆方程为![]() =1.
=1.
又点(1,![]() )在椭圆上,∴
)在椭圆上,∴![]() +
+![]() =1.∴c2=1.∴椭圆的方程为
=1.∴c2=1.∴椭圆的方程为![]() +
+![]() =1.
=1.
(2)设M(x1,y1),N(x2,y2).由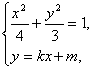 消去y并整理得(3+4k2)x2+8kmx+4m2-12=0.
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0.
∵直线y=kx+m与椭圆有两个交点,Δ=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3.
又x1+x2=![]() ,∴MN中点P的坐标为(
,∴MN中点P的坐标为(![]() ,
,![]() ).
).
设MN的垂直平分线l′方程:y=![]() (x
(x![]() ),∵P在l′上,∴
),∵P在l′上,∴![]() =
=![]() (
(![]() ),
),
即4k2+8km+3=0.∴m=![]() (4k2+3).
(4k2+3).
将上式代入得![]() <4k2+3,∴k2>
<4k2+3,∴k2>![]() ,即k>
,即k>![]() 或k<
或k<![]() .
.
∴k的取值范围为(-∞,![]() )∪(
)∪(![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:选择题
已知椭圆C: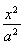 +
+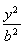 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为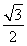 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
(A) 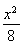 +
+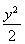 =1 (B)
=1 (B) 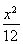 +
+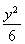 =1
=1
(C) 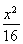 +
+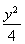 =1 (D)
=1 (D) 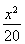 +
+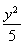 =1
=1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
已知椭圆C: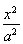 +
+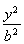 =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
已知椭圆C: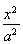 +
+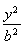 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为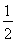 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+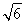 =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)求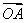 ·
·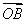 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
已知椭圆C: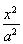 +
+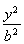 =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P(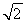 ,
,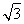 ).
).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,2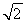 ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com