
【题目】设函数![]() ,若对于在定义域内存在实数
,若对于在定义域内存在实数![]() 满足
满足![]() ,则称函数
,则称函数![]() 为“局部奇函数”.若函数
为“局部奇函数”.若函数![]() 是定义在
是定义在![]() 上的“局部奇函数”,则实数
上的“局部奇函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. [1﹣![]() ,1+
,1+![]() ) B. [﹣1,2] C. [﹣2
) B. [﹣1,2] C. [﹣2![]() ,2
,2![]() ] D. [﹣2
] D. [﹣2![]() ,1﹣
,1﹣![]() ]
]
【答案】B
【解析】根据“局部奇函数”的定义可知,函数f(﹣x)=﹣f(x)有解即可,
即f(﹣x)=4﹣x﹣m2﹣x+m2﹣3=﹣(4x﹣m2x+m2﹣3),
∴4x+4﹣x﹣m(2x+2﹣x)+2m2﹣6=0,
即(2x+2﹣x)2﹣m(2x+2﹣x)+2m2﹣8=0有解即可.
设t=2x+2﹣x,则t=2x+2﹣x≥2,
∴方程等价为t2﹣mt+2m2﹣8=0在t≥2时有解,
设g(t)=t2﹣mt+2m2﹣8,对称轴x=![]() ,
,
①若m≥4,则△=m2﹣4(2m2﹣8)≥0,
即7m2≤32,此时m不存在;
②若m<4,要使t2﹣mt+2m2﹣8=0在t≥2时有解,
则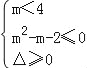 ,解得﹣1≤m<2,综上:﹣1≤m≤2,故选B
,解得﹣1≤m<2,综上:﹣1≤m≤2,故选B


科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣2ax+3为定义在[﹣2,2]上的函数.
(1)当a=1时,求f(x)的最大值与最小值;
(2)若f(x)的最大值为M,最小值为m,函数g(a)=M﹣m,求g(a)的解析式,并求其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次单元测试中,每位同学的考试分数都在区间[100,128]内,将该班所有同学的考试分数分为七组:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],绘制出频率分布直方图如图所示,已知分数低于112分的有18人,则分数不低于120分的人数为( ) 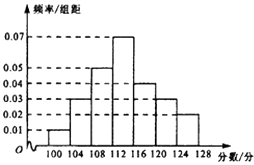
A.10
B.12
C.20
D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数![]() 的图象和直线
的图象和直线![]() 无交点,现有下列结论:
无交点,现有下列结论:
①方程![]() 一定没有实数根;②若
一定没有实数根;②若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
③若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;④若
;④若![]() ,则不等式
,则不等式![]() 对一切实数都成立;⑤函数
对一切实数都成立;⑤函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() ,其导函数为
,其导函数为![]() ,若对任意的实数
,若对任意的实数![]() ,都有
,都有![]() 恒成立,则使
恒成立,则使![]() 成立的实数
成立的实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,m∈R.
,m∈R.
(1)当m=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若f(x)在区间(﹣2,3)上是减函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求证:函数f(x)在实数集R上为增函数;
(2)设g(x)=log2f(x),若关于x的方程g(x)=a有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数:①f(x)=3|x| , ②f(x)=x3 , ③f(x)=ln ![]() ,④f(x)=
,④f(x)= ![]() ,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com