
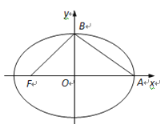
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是椭圆![]() 上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知两个变量线性相关,若它们的相关性越强,则相关系数的绝对值越接近于1.
(2)线性回归直线必过点![]() ;
;
(3)对于分类变量A与B的随机变量![]() ,
,![]() 越大说明“A与B有关系”的可信度越大.
越大说明“A与B有关系”的可信度越大.
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
(5)根据最小二乘法由一组样本点![]() ,求得的回归方程是
,求得的回归方程是![]() ,对所有的解释变量
,对所有的解释变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差.
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
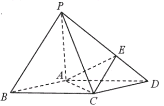
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com