【题目】社区服务是综合实践活动课程的重要内容，某市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据，按时间段
，
，
，
，
（单位：小时）进行统计，其频率分布直方图如图所示.
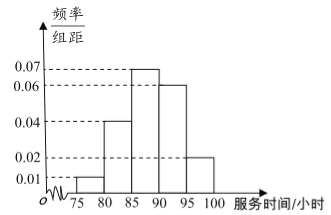
（1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（2）从全市高中学生（人数很多）中任意选取3位学生，记
为3位学生中参加社区服务时间不少于90小时的人数，试求随机变量
的分布列和数学期望
.
【答案】（1）
；（2）分布列见解析，
【解析】
试题分析：（1）由频率分布直方图可求出抽取的
位学生中，参加社区服务时间不少于
小时的学生人数为
人，再根据古典概型概率公式可得结果；（2）随机变量
的可能取值为
分别求出对应的概率，再利用期望公式求解.
试题解析：（1）根据题意，
参加社区服务在时间段
的学生人数为
人；
参加社区服务在时间段
的学生人数为
人；
∴抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为80人.
∴从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率为
.
（2）由（1）可知，从全市高中学生中任意选取1人，其参加社区服务时间不少于90小时的概率为
.
由已知得，随机变量的可能取值为0,1,2,3，
则
，
，
，
，
随机变量
的分布列为
∴
.
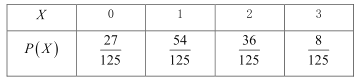
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】设抛物线的顶点在原点，其焦点F在y轴上，又抛物线上的点P(k，－2)与点离
为4，则k等于 ( )
A．4 B．4或－4 C．－2 D．－2或2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有下列说法：①函数y＝－cos 2x的最小正周期是π；
②终边在y轴上的角的集合是{α|α＝
，k∈Z}；
③在同一直角坐标系中，函数y＝sin x的图象和函数y＝x的图象有三个公共点；
④把函数y＝3sin（2x＋
）的图象向右平移
个单位长度得到函数y＝3sin 2x的图象；
⑤函数y＝sin（x－
）在[0，π]上是减函数．
其中，正确的说法是________．（填序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
短轴的一个端点与其两个焦点构成面积为3的直角三角形.
（1）求椭圆
的方程；
（2）过圆
上任意一点
作圆
的切线
， 
与椭圆
交于
两点，以
为直径的圆是否过定点，如过，求出该定点；不过说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】 一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为
，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．
（1）求该几何体的体积
；
（2）求该几何体的表面积
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商店计划每天购进某商品若干件，商店每销售一件该商品可获利润60元，若供大于求，剩余商品全部退回，但每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利40元.
（1）若商品一天购进该商品10件，求当天的利润
（单位：元）关于当天需求量
（单位：件，
）的函数解析式；
（2）商店记录了50天该商品的日需求量
（单位：件，
），整理得下表：
若商店一天购进10件该商品，以50天记录的各需求量的频率作为各需求量发生的概率，求当天的利润在区间
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
