
ЁОЬтФПЁПвбжЊКЏЪ§yЃНf1ЃЈxЃЉЃЌyЃНf2ЃЈxЃЉЃЌЖЈвхКЏЪ§fЃЈxЃЉ ЃЎ
ЃЎ
ЃЈ1ЃЉЩшКЏЪ§f1ЃЈxЃЉЃНx+3ЃЌf2ЃЈxЃЉЃНx2ЉxЃЌЧѓКЏЪ§yЃНfЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌgЃЈxЃЉЃНmx+2ЃЈmЁЪRЃЉЃЌКЏЪ§hЃЈxЃЉЃНfЃЈxЃЉЉgЃЈxЃЉгаШ§ИіВЛЭЌЕФСуЕуЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшКЏЪ§f1ЃЈxЃЉЃНx2Љ2ЃЌf2ЃЈxЃЉЃН|xЉa|ЃЌКЏЪ§FЃЈxЃЉЃНf1ЃЈxЃЉ+f2ЃЈxЃЉЃЌЧѓКЏЪ§FЃЈxЃЉЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ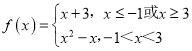 ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ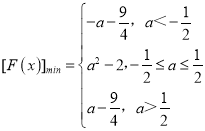
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнКЏЪ§fЃЈxЃЉ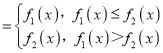 ЕФЖЈвхЃЌСНИіКЏЪ§жаШЁаЁЕФ.
ЕФЖЈвхЃЌСНИіКЏЪ§жаШЁаЁЕФ.
ЃЈ2ЃЉКЏЪ§hЃЈxЃЉЃНfЃЈxЃЉЉgЃЈxЃЉгаШ§ИіВЛЭЌЕФСуЕуЃЌМДЗНГЬfЃЈxЃЉЃНgЃЈxЃЉгаШ§ИіВЛЭЌЕФЪЕЪ§ИљЃЌвђЮЊКЏЪ§![]() ЪЧЗжЖЮКЏЪ§ЃЌЗжРрЬжТлЃЌЗжБ№гУвЛДЮЗНГЬКЭЖўДЮЗНГЬЧѓНт.
ЪЧЗжЖЮКЏЪ§ЃЌЗжРрЬжТлЃЌЗжБ№гУвЛДЮЗНГЬКЭЖўДЮЗНГЬЧѓНт.
ЃЈ3ЃЉИљОнЬтвтFЃЈxЃЉ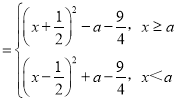 ЃЎАДееЖўДЮКЏЪ§КЏЪ§ЖЈЧјМфЖЏЕФРраЭЃЌЬжТлЖдГЦжсгыЧјМфЖЫЕужЕМфЕФЙиЯЕЧѓзюжЕ.
ЃЎАДееЖўДЮКЏЪ§КЏЪ§ЖЈЧјМфЖЏЕФРраЭЃЌЬжТлЖдГЦжсгыЧјМфЖЫЕужЕМфЕФЙиЯЕЧѓзюжЕ.
ЃЈ1ЃЉЁпf1ЃЈxЃЉЃНx+3ЃЌ![]() ЃЌ
ЃЌ
ЕБf1ЃЈxЃЉЁмf2ЃЈxЃЉЃЌМДxЁн3ЛђxЁмЉ1ЪБЃЌfЃЈxЃЉЃНx+3ЃЌ
ЕБf1ЃЈxЃЉЃОf2ЃЈxЃЉЃЌМДЉ1ЃМxЃМ3ЪБЃЌ![]() ЃЌ
ЃЌ
злЩЯЃК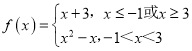 ЃЎ
ЃЎ
ЃЈ2ЃЉКЏЪ§hЃЈxЃЉЃНfЃЈxЃЉЉgЃЈxЃЉгаШ§ИіВЛЭЌЕФСуЕуЃЌ
МДЗНГЬfЃЈxЃЉЃНgЃЈxЃЉгаШ§ИіВЛЭЌЕФЪЕЪ§ИљЃЌ
вђЮЊКЏЪ§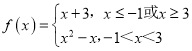 ЃЌКЏЪ§gЃЈxЃЉЃНmx+2ЃЈmЁЪRЃЉЃЌ
ЃЌКЏЪ§gЃЈxЃЉЃНmx+2ЃЈmЁЪRЃЉЃЌ
ЫљвдЕБxЁмЉ1ЛђxЁн3ЪБЃЌmx+2ЃНx+3ЧЁгавЛИіЪЕЪ§НтЃЌ
Ыљвд![]() Лђ
Лђ![]() ЃЌ
ЃЌ
НтЕУЃЌ![]() ЃЎ
ЃЎ
ЕБЉ1ЃМxЃМ3ЪБЃЌmx+2ЃНx2ЉxЧЁгаСНИіВЛЭЌЕФЪЕЪ§НтЃЌ
МДЕБЉ1ЃМxЃМ3ЪБx2ЉЃЈm+1ЃЉxЉ2=0ЧЁгаСНИіВЛЭЌЕФЪЕЪ§НтЃЌ
ЩшКЏЪ§hЃЈxЃЉЃНx2ЉЃЈm+1ЃЉxЉ2ЃЌ
гЩЬтвтПЩЕУ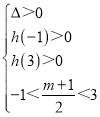 ЃЌ
ЃЌ
Ыљвд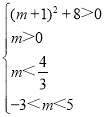 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
злЩЯЃЌmЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉFЃЈxЃЉЃНf1ЃЈxЃЉ+f2ЃЈxЃЉЃНx2+|xЉa|Љ2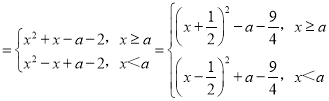 ЃЎ
ЃЎ
ЂйШєa![]() ЃЌдђКЏЪ§FЃЈxЃЉдк
ЃЌдђКЏЪ§FЃЈxЃЉдк![]() ЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдк
ЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдк![]() ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ДЫЪБЃЌКЏЪ§FЃЈxЃЉЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЂкШє![]() ЃЌдђКЏЪ§FЃЈxЃЉдкЃЈЉЁоЃЌaЃЉЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдкЃЈaЃЌ+ЁоЃЉЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ЃЌдђКЏЪ§FЃЈxЃЉдкЃЈЉЁоЃЌaЃЉЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдкЃЈaЃЌ+ЁоЃЉЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ДЫЪБЃЌКЏЪ§FЃЈxЃЉЕФзюаЁжЕЮЊFЃЈaЃЉЃНa2Љ2ЃЛ
ЂлШє![]() ЃЌдђКЏЪ§FЃЈxЃЉдк
ЃЌдђКЏЪ§FЃЈxЃЉдк![]() ЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдк
ЩЯЪЧЕЅЕїМѕКЏЪ§ЃЌдк![]() ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ЩЯЪЧЕЅЕїдіКЏЪ§ЃЌ
ДЫЪБЃЌКЏЪ§FЃЈxЃЉЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
злЩЯЃК ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫЕЗЈЃК
ЂйШєжБЯп![]() ЦНаагкЦНУц
ЦНаагкЦНУц![]() ФкЕФЮоЪ§ЬѕжБЯпЃЌдђ
ФкЕФЮоЪ§ЬѕжБЯпЃЌдђ![]() ЃЛ
ЃЛ
ЂкШєжБЯп![]() дкЦНУц
дкЦНУц![]() ЭтЃЌдђ
ЭтЃЌдђ![]() ЃЛ
ЃЛ
ЂлШєжБЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() ЦНУц
ЦНУц![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂмШєжБЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() ЦНУц
ЦНУц![]() ЃЌдђжБЯп
ЃЌдђжБЯп![]() ЦНаагкЦНУц
ЦНаагкЦНУц![]() ФкЕФЮоЪ§ЬѕжБЯп.
ФкЕФЮоЪ§ЬѕжБЯп.
Цфжае§ШЗЫЕЗЈЕФИіЪ§ЮЊЃЈ ЃЉ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗжагавЛЗжТЙЮЪЬтЃКЁАНёгаДѓЗђЁЂВЛИќЁЂєЂєСЁЂЩЯдьЁЂЙЋЪПЃЌЗВЮхШЫЃЌЙВСдЕУЮхТЙЃЎгћвдОєДЮЗжжЎЃЌЮЪИїЕУМИКЮЃЎЁБдкетИіЮЪЬтжаЃЌДѓЗђЁЂВЛИќЁЂєЂєСЁЂЩЯдьЁЂЙЋЪПЪЧЙХДњЮхИіВЛЭЌОєДЮЕФЙйдБЃЌЯжЛЪЕлНЋДѓЗђЁЂВЛИќЁЂєЂшЩЁЂЩЯдьЁЂЙЋЪПет5ШЫЗжГЩ3зщХЩШЅШ§ЕижДааЙЋЮёЃЈУПЕижСЩйШЅ1ШЫЃЉЃЌдђВЛЭЌЕФЗНАИгаЃЈ ЃЉжжЃЎ
A.150B.180C.240D.300
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§yЃНfЃЈxЃЉЃЌШєдкЦфЖЈвхгђФкДцдкx0ЃЌЪЙЕУx0fЃЈx0ЃЉЃН1ГЩСЂЃЌдђГЦКЏЪ§fЃЈxЃЉОпгааджЪMЃЎ
ЃЈ1ЃЉЯТСаКЏЪ§жаОпгааджЪMЕФга____
ЂйfЃЈxЃЉЃНЉx+2
ЂкfЃЈxЃЉЃНsinxЃЈxЁЪ[0ЃЌ2Іа]ЃЉ
ЂлfЃЈxЃЉЃНx![]() ЃЌЃЈxЁЪЃЈ0ЃЌ+ЁоЃЉЃЉ
ЃЌЃЈxЁЪЃЈ0ЃЌ+ЁоЃЉЃЉ
ЂмfЃЈxЃЉ![]()
ЃЈ2ЃЉШєКЏЪ§fЃЈxЃЉЃНaЃЈ|xЉ2|Љ1ЃЉЃЈxЁЪ[Љ1ЃЌ+ЁоЃЉЃЉОпгааджЪMЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯђСП![]() ЃЈ2sinxЃЌcosxЃЉЃЌ
ЃЈ2sinxЃЌcosxЃЉЃЌ![]() ЃЈ
ЃЈ![]() cosxЃЌ2cosxЃЉЃЎ
cosxЃЌ2cosxЃЉЃЎ
ЃЈ1ЃЉШєxЁйkІа![]() ЃЌkЁЪZЃЌЧв
ЃЌkЁЪZЃЌЧв![]() ЃЌЧѓ2sin2xЉcos2xЕФжЕЃЛ
ЃЌЧѓ2sin2xЉcos2xЕФжЕЃЛ
ЃЈ2ЃЉЖЈвхКЏЪ§fЃЈxЃЉ![]() ЃЌЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЕнМѕЧјМфЃЛВЂЧѓЕБxЁЪ[0ЃЌ
ЃЌЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЕнМѕЧјМфЃЛВЂЧѓЕБxЁЪ[0ЃЌ![]() ]ЪБЃЌКЏЪ§fЃЈxЃЉЕФжЕгђЃЎ
]ЪБЃЌКЏЪ§fЃЈxЃЉЕФжЕгђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018ФъжаЧяМОЕНРДжЎМЪЃЌФГГЌЪаЮЊСЫНтжаЧяНкЦкМфдТБ§ЕФЯњЪлСПЃЌЖдЦфЫљдкЯњЪлЗЖЮЇФкЕФ1000УћЯћЗбепдкжаЧяНкЦкМфЕФдТБ§ЙКТђСПЃЈЕЅЮЛЃК![]() ЃЉНјааСЫЮЪОэЕїВщЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃК
ЃЉНјааСЫЮЪОэЕїВщЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃК

ЃЈ1ЃЉЧѓЦЕТЪЗжВМжБЗНЭМжа![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊИУГЌЪаЫљдкЯњЪлЗЖЮЇФкга20ЭђШЫЃЌВЂЧвИУГЌЪаУПФъЕФЯњЪлЗнЖюдМеМИУЪаГЁзмСПЕФ![]() ЃЌЧыИљОнШЫОљдТБ§ЙКТђСПЙРМЦИУГЌЪагІзМБИЖрЩйЖждТБ§ЧЁКУФмТњзуЪаГЁашЧѓЃП
ЃЌЧыИљОнШЫОљдТБ§ЙКТђСПЙРМЦИУГЌЪагІзМБИЖрЩйЖждТБ§ЧЁКУФмТњзуЪаГЁашЧѓЃП
ЃЈ3ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩвдШЯЮЊЃЌИУЯњЪлЗЖЮЇФкЯћЗбепЕФдТБ§ЙКТђСП![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌЦфжабљБОЦНОљЪ§
ЃЌЦфжабљБОЦНОљЪ§![]() зїЮЊ
зїЮЊ![]() ЕФЙРМЦжЕЃЌбљБОБъзМВю
ЕФЙРМЦжЕЃЌбљБОБъзМВю![]() зїЮЊ
зїЮЊ![]() ЕФЙРМЦжЕЃЌЩш
ЕФЙРМЦжЕЃЌЩш![]() БэЪОДгИУЯњЪлЗЖЮЇФкЕФЯћЗбепжаЫцЛњГщШЁ10УћЃЌЦфдТБ§ЙКТђСПЮЛгк
БэЪОДгИУЯњЪлЗЖЮЇФкЕФЯћЗбепжаЫцЛњГщШЁ10УћЃЌЦфдТБ§ЙКТђСПЮЛгк![]() ЕФШЫЪ§ЃЌЧѓ
ЕФШЫЪ§ЃЌЧѓ![]() ЕФЪ§бЇЦкЭћ.
ЕФЪ§бЇЦкЭћ.
ИНЃКОМЦЫуЕУ![]() ЃЌШєЫцЛњБфСП
ЃЌШєЫцЛњБфСП![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЦкЃЌФГбЇаЃОйааСЫвЛДЮЬхг§жЊЪЖОКШќЃЌВЂЖдОКШќГЩМЈНјааЗжзщЃКГЩМЈВЛЕЭгк80ЗжЕФбЇЩњЮЊМззщЃЌГЩМЈЕЭгк80ЗжЕФбЇЩњЮЊввзщ.ЮЊСЫЗжЮіОКШќГЩМЈгыадБ№ЪЧЗёгаЙиЃЌЯжЫцЛњГщШЁСЫ60УћбЇЩњЕФГЩМЈНјааЗжЮіЃЌЪ§ОнШчЯТЭМЫљЪОЕФ![]() СаСЊБэ.
СаСЊБэ.
Мззщ | ввзщ | КЯМЦ | |
ФаЩњ | 3 | ||
ХЎЩњ | 13 | ||
КЯМЦ | 40 | 60 |
ЃЈ1ЃЉНЋ![]() СаСЊБэВЙГфЭъећЃЌХаЖЯЪЧЗёга
СаСЊБэВЙГфЭъећЃЌХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊбЇЩњАДГЩМЈЗжзщгыадБ№гаЙиЃП
ЕФАбЮеШЯЮЊбЇЩњАДГЩМЈЗжзщгыадБ№гаЙиЃП
ЃЈ2ЃЉШчЙћгУЗжВуГщбљЕФЗНЗЈДгМззщКЭввзщжаГщШЁ6ШЫЃЌдйДгет6ШЫжаЫцЛњГщШЁ2ШЫЃЌЧѓжСЩйга1ШЫдкМззщЕФИХТЪ.
ИНЃК ЃЌ
ЃЌ![]() .
.
ВЮПМЪ§ОнМАЙЋЪНЃК
| 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЮвЙњОМУЕФЗЂеЙЃЌОгУёЪеШыж№ФъдіГЄЃЎФГЕиЧј2014ФъжС2018ФъХЉДхОгУёМвЭЅШЫОљДПЪеШы![]() ЃЈЕЅЮЛЃКЧЇдЊЃЉЕФЪ§ОнШчЯТБэЃК
ЃЈЕЅЮЛЃКЧЇдЊЃЉЕФЪ§ОнШчЯТБэЃК
ФъЗн | 2014 | 2015 | 2016 | 2017 | 2018 |
ФъЗнДњКХ | 1 | 2 | 3 | 4 | 5 |
ШЫОљДПЪеШы | 5 | 6 | 7 | 8 | 10 |
ЃЈ1ЃЉЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЛ
ЕФЯпадЛиЙщЗНГЬЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌЗжЮі2014ФъжС2018ФъИУЕиЧјХЉДхОгУёМвЭЅШЫОљДПЪеШыЕФБфЛЏЧщПіЃЌВЂдЄВт2020ФъИУЕиЧјХЉДхОгУёМвЭЅШЫОљДПЪеШыдМЮЊЖрЩйЧЇдЊЃП
ИНЃКЛиЙщжБЯпЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊ ЃЌ
ЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФжааФЮЊдЕу
ЕФжааФЮЊдЕу![]() ЃЌГЄжсдк
ЃЌГЄжсдк![]() жсЩЯЃЌзѓЖЅЕуЮЊ
жсЩЯЃЌзѓЖЅЕуЮЊ![]() ЃЌЩЯЁЂЯТНЙЕуЗжБ№ЮЊ
ЃЌЩЯЁЂЯТНЙЕуЗжБ№ЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФжаЕуЗжБ№ЮЊ
ЕФжаЕуЗжБ№ЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЪЧаББпГЄЮЊ
ЪЧаББпГЄЮЊ![]() ЕФжБНЧШ§НЧаЮ.
ЕФжБНЧШ§НЧаЮ.
ЃЈ1ЃЉШєЕу![]() дкЭждВ
дкЭждВ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЮЊШёНЧЃЌЧѓ
ЮЊШёНЧЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЙ§Еу![]() зїжБЯпНЛЭждВ
зїжБЯпНЛЭждВ![]() гкЕу
гкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com