
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,若方程
时,若方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上是减函数;当
上是减函数;当![]() 时,
时,![]() 在
在![]() 上是增函数;(3)证明见解析.
上是增函数;(3)证明见解析.
【解析】
(1)当![]() 时,
时,![]() ,求得其导函数
,求得其导函数 ![]() ,
,![]() ,可求得函数
,可求得函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)由已知得![]() ,得出导函数
,得出导函数![]() ,并得出导函数取得正负的区间,可得出函数的单调性;
,并得出导函数取得正负的区间,可得出函数的单调性;
(3)当![]() 时,
时,![]() ,
,![]() ,由(2)得
,由(2)得![]() 的单调区间,以当方程
的单调区间,以当方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,不妨设
,不妨设![]() ,且有
,且有![]() ,
,![]() ,构造函数
,构造函数![]() ,分析其导函数的正负得出函数的单调性,得出其最值,所证的不等式可得证.
,分析其导函数的正负得出函数的单调性,得出其最值,所证的不等式可得证.
(1)当![]() 时,
时,![]() ,
,
所以 ![]() ,
,![]() ,
,
所以函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ;
;
(2)由已知得![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(3)当![]() 时,
时,![]() ,
,![]() ,由(2)得
,由(2)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
所以![]() ,且
,且![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
所以当方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,不妨设
,不妨设![]() ,且有
,且有![]() ,
,![]() ,
,
构造函数![]() ,则
,则![]() ,
,
当![]() 时,
时,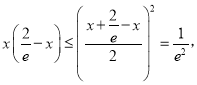 所以
所以![]() ,
,
![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,![]() ,
,
由![]()
![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() .
.
所以![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,以下结论正确的个数为( )
,以下结论正确的个数为( )
①当![]() 时,函数
时,函数![]() 的图象的对称中心为
的图象的对称中心为![]() ;
;
②当![]() 时,函数
时,函数![]() 在
在![]() 上为单调递减函数;
上为单调递减函数;
③若函数![]() 在
在![]() 上不单调,则
上不单调,则![]() ;
;
④当![]() 时,
时,![]() 在
在![]() 上的最大值为15.
上的最大值为15.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为14万元/辆,年销售量为![]() 辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为
辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为![]() (0<
(0<![]() <1),则出厂价相应提高的比例为0.6
<1),则出厂价相应提高的比例为0.6![]() ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.5![]() ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例![]() 应在什么范围内?
应在什么范围内?
(2)若年销售量关于![]() 的函数为
的函数为![]() 为常数),则当
为常数),则当![]() 为何值时,本年度的年利润最大?
为何值时,本年度的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根据正弦定理把![]() 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
根据正弦定理,![]() 可化为
可化为![]()
∵△ABC的周长为![]() ,
,
∴联立方程组![]() ,
,
解得a=2.
故选:B
【点睛】
(1)在三角形中根据已知条件求未知的边或角时,要灵活选择正弦、余弦定理进行边角之间的转化,以达到求解的目的.
(2)求角的大小时,在得到角的某一个三角函数值后,还要根据角的范围才能确定角的大小,这点容易被忽视,解题时要注意.
【题型】单选题
【结束】
7
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说,年过半百的笛卡尔担任瑞典一小公国的公主克里斯蒂娜的数学老师,日久生情,彼此爱慕,其父国王知情后大怒,将笛卡尔流放回法国,并软禁公主,笛卡尔回法国后染上黑死病,连连给公主写信,死前最后一封信只有一个公式:![]()
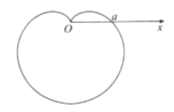
![]() 国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系
国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系![]() 中,方程
中,方程![]()
![]() 表示的曲线
表示的曲线![]() 就是一条心形线,如图,以极轴
就是一条心形线,如图,以极轴![]() 所在直线为
所在直线为![]() 轴,极点
轴,极点![]() 为坐标原点的直角坐标系
为坐标原点的直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为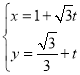 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三点,求线段
三点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
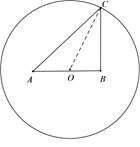
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,![]() 两点为喷泉,圆心
两点为喷泉,圆心![]() 为
为![]() 的中点,其中
的中点,其中![]() 米,半径
米,半径![]() 米,市民可位于水池边缘任意一点
米,市民可位于水池边缘任意一点![]() 处观赏.
处观赏.
(1)若当![]() 时,
时,![]() ,求此时
,求此时![]() 的值;
的值;
(2)设![]() ,且
,且![]() .
.
(i)试将![]() 表示为
表示为![]() 的函数,并求出
的函数,并求出![]() 的取值范围;
的取值范围;
(ii)若同时要求市民在水池边缘任意一点![]() 处观赏喷泉时,观赏角度
处观赏喷泉时,观赏角度![]() 的最大值不小于
的最大值不小于![]() ,试求
,试求![]() 两处喷泉间距离的最小值.
两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数,
为参数, ![]() ),将曲线
),将曲线![]() 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线![]() .
.
(1)以原点为极点, ![]() 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() (
(![]() 为参数)与
为参数)与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com