
【题目】已知函数![]() .
.
(1)若曲线![]() 的切线方程为
的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据解析式求得导函数,设切点坐标为![]() ,结合导数的几何意义可得方程
,结合导数的几何意义可得方程![]() ,构造函数
,构造函数![]() ,并求得
,并求得![]() ,由导函数求得
,由导函数求得![]() 有最小值
有最小值![]() ,进而可知由唯一零点
,进而可知由唯一零点![]() ,即可代入求得
,即可代入求得![]() 的值;
的值;
(2)将![]() 解析式代入
解析式代入![]() ,结合零点定义化简并分离参数得
,结合零点定义化简并分离参数得![]() ,构造函数
,构造函数![]() ,根据题意可知直线
,根据题意可知直线![]() 与曲线
与曲线![]() 有两个交点;求得
有两个交点;求得![]() 并令
并令![]() 求得极值点,列出表格判断
求得极值点,列出表格判断![]() 的单调性与极值,即可确定与
的单调性与极值,即可确定与![]() 有两个交点时
有两个交点时![]() 的取值范围.
的取值范围.
(1)依题意,![]() ,
,![]() ,
,
设切点为![]() ,
,![]() ,
,
故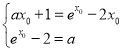 ,
,
故![]() ,则
,则![]() ;
;
令![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故当![]() 时,函数
时,函数![]() 有最小值,
有最小值,
由于![]() ,故
,故![]() 有唯一实数根0,
有唯一实数根0,
即![]() ,则
,则![]() ;
;
(2)由![]() ,得
,得![]() .
.
所以“![]() 在区间
在区间![]() 上有两个零点”等价于“直线
上有两个零点”等价于“直线![]() 与曲线
与曲线![]() 在
在![]() 有两个交点”;
有两个交点”;
由于![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
| 3 |
|
|
| 0 | + | 0 |
|
|
| 极小值 |
| 极大值 |
|
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又因为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故当![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 上有两个交点,
上有两个交点,
即当![]() 或
或![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() , 以
, 以![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴, 建立平面直角坐标系
轴, 建立平面直角坐标系![]() , 如图所示, 山区边界曲线为
, 如图所示, 山区边界曲线为![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,![]() 的横坐标为
的横坐标为![]() .
.
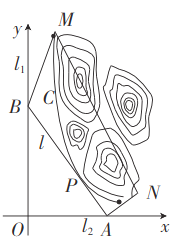
(1)当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度;
的长度最短?求出最短长度;
(2)当公路![]() 的长度最短时,设公路
的长度最短时,设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,并测得四边形
两点,并测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,该项质量指标值落在区间![]() 内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
图:设备改造前样本的频率分布直方图
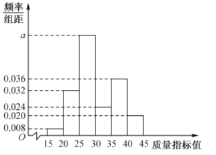
表:设备改造后样本的频率分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)求图中实数![]() 的值;
的值;
(2)企业将不合格品全部销毁后,对合格品进行等级细分,质量指标值落在区间![]() 内的定为一等品,每件售价240元;质量指标值落在区间
内的定为一等品,每件售价240元;质量指标值落在区间![]() 或
或![]() 内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为
内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每日健步走的步数,从而为科学健身提供了一定帮助.某企业为了解员工每日健步走的情况,从该企业正常上班的员工中随机抽取300名,统计他们的每日健步走的步数(均不低于4千步,不超过20千步).按步数分组,得到频率分布直方图如图所示.
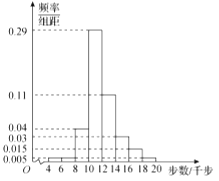
(1)求这300名员工日行步数![]() (单位:千步)的样本平均数(每组数据以该组区间的中点值为代表,结果保留整数);
(单位:千步)的样本平均数(每组数据以该组区间的中点值为代表,结果保留整数);
(2)由直方图可以认为该企业员工的日行步数![]() (单位:千步)服从正态分布
(单位:千步)服从正态分布![]() ,其中
,其中![]() 为样本平均数,标准差
为样本平均数,标准差![]() 的近似值为2,求该企业被抽取的300名员工中日行步数
的近似值为2,求该企业被抽取的300名员工中日行步数![]() 的人数;
的人数;
(3)用样本估计总体,将频率视为概率.若工会从该企业员工中随机抽取2人作为“日行万步”活动的慰问奖励对象,规定:日行步数不超过8千步者为“不健康生活方式者”,给予精神鼓励,奖励金额为每人0元;日行步数为8~14千步者为“一般生活方式者”,奖励金额为每人100元;日行步数为14千步以上者为“超健康生活方式者”,奖励金额为每人200元.求工会慰问奖励金额![]() (单位:元)的分布列和数学期望.
(单位:元)的分布列和数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销,定价为![]() 元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照
元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到如下频率分布直方图,以不同销量的频率估计概率.
分组,得到如下频率分布直方图,以不同销量的频率估计概率.
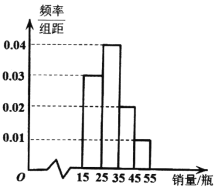
![]() 从试销售期间任选三天,求其中至少有一天的酸奶销量大于
从试销售期间任选三天,求其中至少有一天的酸奶销量大于![]() 瓶的概率;
瓶的概率;
![]() 试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱
试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元;小箱每箱
元;小箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为
元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为![]() 时看作销量为
时看作销量为![]() 瓶).
瓶).
①设早餐店批发一大箱时,当天这款酸奶的利润为随机变量![]() ,批发一小箱时,当天这款酸奶的利润为随机变量
,批发一小箱时,当天这款酸奶的利润为随机变量![]() ,求
,求![]() 和
和![]() 的分布列和数学期望;
的分布列和数学期望;
②以利润作为决策依据,该早餐店应每天批发一大箱还是一小箱?
注:销售额=销量×定价;利润=销售额-批发成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 为短轴端点,且
为短轴端点,且![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程,
的方程,
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点![]() ,
,![]() ,且满足
,且满足![]() ?若存在,求出该圆的方程,若不存在,说明理由.
?若存在,求出该圆的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又称十二属相,中国古人拿十二种动物来配十二地支,组成子鼠、丑牛、寅虎、卯兔、辰龙、已蛇、午马、未羊、申猴、西鸡、戌狗、亥猪十二属相现有十二生肖吉祥物各一件,甲、乙、丙三位同学依次随机抽取一件作为礼物,甲同学喜欢马、牛,乙同学喜欢马、龙、狗,丙同学除了鼠不喜欢外其他的都喜欢,则这三位同学抽取的礼物都喜欢的概率是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com