
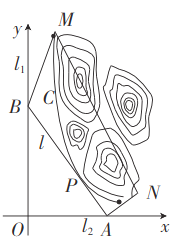
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() , 以
, 以![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴, 建立平面直角坐标系
轴, 建立平面直角坐标系![]() , 如图所示, 山区边界曲线为
, 如图所示, 山区边界曲线为![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,![]() 的横坐标为
的横坐标为![]() .
.
(1)当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度;
的长度最短?求出最短长度;
(2)当公路![]() 的长度最短时,设公路
的长度最短时,设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,并测得四边形
两点,并测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
【答案】(1)当![]() 时,公路
时,公路![]() 的长度最短为
的长度最短为![]() 千米;(2)
千米;(2)![]() (千米).
(千米).
【解析】
(1)设切点![]() 的坐标为
的坐标为![]() ,利用导数的几何意义求出切线
,利用导数的几何意义求出切线![]() 的方程为
的方程为![]() ,根据两点间距离得出
,根据两点间距离得出![]() ,构造函数
,构造函数![]() ,利用导数求出单调性,从而得出极值和最值,即可得出结果;
,利用导数求出单调性,从而得出极值和最值,即可得出结果;
(2)在![]() 中,由余弦定理得出
中,由余弦定理得出![]() ,利用正弦定理
,利用正弦定理![]() ,求出
,求出![]() ,最后根据勾股定理即可求出
,最后根据勾股定理即可求出![]() 的长度.
的长度.
(1)由题可知,设点![]() 的坐标为
的坐标为![]() ,
,
又![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
由此得直线![]() 与坐标轴交点为:
与坐标轴交点为:![]() ,
,
则![]() ,故
,故![]() ,
,
设![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() =10.
=10.
当![]() 时,
时,![]() 是减函数;
是减函数;
当![]() 时,
时,![]() 是增函数.
是增函数.
所以当![]() 时,函数
时,函数![]() 有极小值,也是最小值,
有极小值,也是最小值,
所以![]() , 此时
, 此时![]() .
.
故当![]() 时,公路
时,公路![]() 的长度最短,最短长度为
的长度最短,最短长度为![]() 千米.
千米.
(2) 在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
根据正弦定理
![]() ,
,
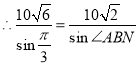 ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理可得![]() ,
,
即![]() ,
,
解得,![]() (千米).
(千米).


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)解关于![]() 的不等式:
的不等式:![]() ;
;
(2)当![]() 时,过点
时,过点![]() 是否存在函数
是否存在函数![]() 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,试比较
恒成立的最小值,试比较![]() 与
与![]() 的大小(
的大小(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量![]() ,
,![]() 满足:|
满足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)设向量![]() ,
,![]() 的夹角为θ.若存在t∈R,使得
的夹角为θ.若存在t∈R,使得![]() ,求cosθ的取值范围.
,求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() .已知当
.已知当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,
,![]() .
.
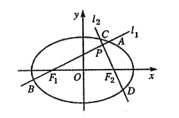
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 点坐标并求出此定值;若不存在,说明理由.
点坐标并求出此定值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,从而得椭圆的方程,第二问由题目分析如果存两定点,则
,从而得椭圆的方程,第二问由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把
点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把![]() 坐标化,求得
坐标化,求得![]() 点的轨迹方程是椭圆
点的轨迹方程是椭圆![]() ,从而求得存在两定点
,从而求得存在两定点![]() 和点
和点![]() .
.
【题型】解答题
【结束】
21
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我区的中小学办学条件在政府的教育督导下,迅速得到改变.督导一年后.分别随机抽查了高中(用![]() 表示)与初中(用
表示)与初中(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
①高中得分与初中得分的优秀率相同
②高中得分与初中得分的中位数相同
③高中得分的方差比初中得分的方差大
④高中得分与初中得分的平均分相同
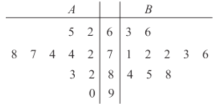
A.①②B.①③C.②④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com