
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: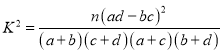 .
.
|
|
|
|
|
|
|
|
科目:高中数学 来源: 题型:
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
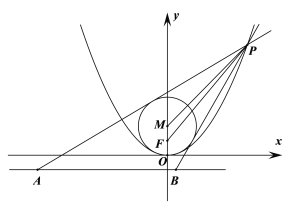
【题目】如图,点![]() 是抛物线
是抛物线![]() 上位于第一象限内一动点,
上位于第一象限内一动点,![]() 是焦点,圆
是焦点,圆![]() :
:![]() ,过点
,过点![]() 作圆
作圆![]() 的切线交准线于
的切线交准线于![]() ,
,![]() 两点.
两点.
(Ⅰ)记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 的横坐标
的横坐标![]() ,求
,求![]() 面积
面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
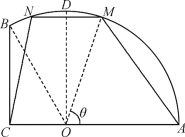
【题目】某处有一块闲置用地,如图所示,它的边界由圆O的一段圆弧![]() 和两条线段
和两条线段![]() ,
,![]() 构成.已知圆心O在线段
构成.已知圆心O在线段![]() 上,现测得圆O半径为2百米,
上,现测得圆O半径为2百米,![]() ,
,![]() .现规划在这片闲置用地内划出一片梯形区域用于商业建设,该梯形区域的下底为
.现规划在这片闲置用地内划出一片梯形区域用于商业建设,该梯形区域的下底为![]() ,上底为
,上底为![]() ,点M在圆弧
,点M在圆弧![]() (点D在圆弧
(点D在圆弧![]() 上,且
上,且![]() )上,点N在圆弧
)上,点N在圆弧![]() 上或线段
上或线段![]() 上.设
上.设![]() .
.
(1)将梯形![]() 的面积表示为
的面积表示为![]() 的函数;
的函数;
(2)当![]() 为何值时,梯形
为何值时,梯形![]() 的面积最大?求出最大面积.
的面积最大?求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.
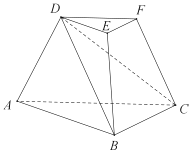
(I)证明:EF⊥DB;
(II)求DF与面DBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
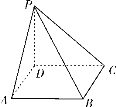
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中,![]() 为矩形,
为矩形,![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
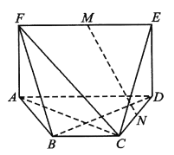
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求多面体
,求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com