
【题目】已知过抛物线![]() 焦点
焦点![]() 且倾斜角的
且倾斜角的![]() 直线
直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]()
![]() 的面积为
的面积为![]() .
.
(I)求抛物线![]() 的方程;
的方程;
(II)设![]() 是直线
是直线![]() 上的一个动点,过
上的一个动点,过![]() 作抛物线
作抛物线![]() 的切线,切点分别为
的切线,切点分别为![]() 直线
直线![]() 与直线
与直线![]() 轴的交点分别为
轴的交点分别为![]() 点
点![]() 是以
是以![]() 为圆心
为圆心![]() 为半径的圆上任意两点,求
为半径的圆上任意两点,求![]() 最大时点
最大时点![]() 的坐标.
的坐标.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题
(I)抛物线焦点为![]() ,写出直线
,写出直线![]() 方程,与抛物线方程联立,消元后可得
方程,与抛物线方程联立,消元后可得![]() ,其中
,其中![]() ,可再求出原点
,可再求出原点![]() 到直线
到直线![]() 的距离
的距离![]() ,由
,由![]() 求得
求得![]() ,也可由
,也可由![]() 求得
求得![]() ;
;
(II)首先设出点坐标,设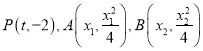 ,利用导数的几何意义得出两切线方程,代入
,利用导数的几何意义得出两切线方程,代入![]() 点坐标,从而得直线
点坐标,从而得直线![]() 方程为
方程为![]() ,从而可得
,从而可得![]() 坐标,得
坐标,得![]() 的长,而要使
的长,而要使![]() 最大,则
最大,则![]() 与圆
与圆![]() 相切,这样可求得
相切,这样可求得![]() ,最后由基本不等式可得最大值.也可用正切函数求最大值.
,最后由基本不等式可得最大值.也可用正切函数求最大值.
试题解析:
(I)依题意,![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ;
;
由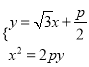 得
得![]() ,
,
![]()
所以![]() ,
,
![]() 到
到![]() 的距离
的距离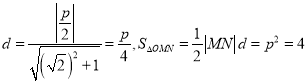 ,
,
![]() ,抛物线方程为
,抛物线方程为![]()
(II)设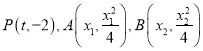 ,由
,由![]() 得
得![]() ,
,
则切线![]() 方程为
方程为![]() 即
即![]() ,
,
同理,切线![]() 方程为
方程为![]() ,
,
把![]() 代入可得
代入可得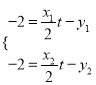 故直线
故直线![]() 的方程为
的方程为![]() 即
即![]()
![]() 由
由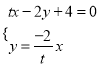 得
得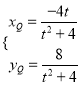 ,
,
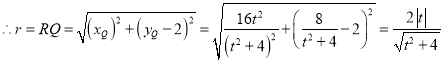 ,
,
当![]() 与圆
与圆![]() 相切时角
相切时角![]() 最大,
最大,
此时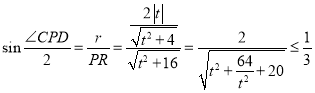 ,等号当
,等号当![]() 时成立
时成立
![]() 当
当![]() 时,所求的角
时,所求的角![]() 最大.
最大.
综上,当![]() 最大时点
最大时点![]() 的坐标为
的坐标为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并说明理由.①
,并说明理由.①![]() ;②
;②![]() .
.
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() ,求证:对任意
,求证:对任意![]() 有
有![]() ;
;
(3)在(2)的条件下,是否对任意![]() 均有
均有![]() .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的是( )
处取得最大值,则下列命题正确的是( )
①当![]() 时,
时,![]() 的取值范围是
的取值范围是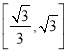 ;
;
②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;
个单位后所对应的函数为偶函数;
③函数![]() 的最小正周期为
的最小正周期为![]() ;
;
④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.①②B.①③C.①③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.

(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场春节期间推出一项优惠活动,活动规则如下:消费额每满300元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在区域Ⅰ返券60元;停在区域Ⅱ返券30元;停在区域Ⅲ不返券.例如:消费600元,可抽奖2次,所获得的返券金额是两次金额之和.
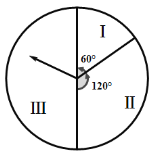
(Ⅰ)若某位顾客消费300元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费600元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com