
【题目】在三棱锥![]() 中,
中,![]() ,二面角
,二面角![]() 、
、![]() 、
、![]() 的大小均为
的大小均为![]() ,设三棱锥
,设三棱锥![]() 的外接球球心为
的外接球球心为![]() ,直线
,直线![]() 交平面
交平面![]() 于点
于点![]() ,则三棱锥
,则三棱锥![]() 的内切球半径为_______________,
的内切球半径为_______________,![]() __________
__________
【答案】![]()
![]()
【解析】
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,则由已知
,则由已知![]() 是
是![]() 内心,由直角三角形的性质求得内切圆半径从而可得
内心,由直角三角形的性质求得内切圆半径从而可得![]() ,由此用体积法求得内切球半径,过斜边中点
,由此用体积法求得内切球半径,过斜边中点![]() 作平面
作平面![]() 的垂线,则外接球球心在此垂线上,只是要确定在平面
的垂线,则外接球球心在此垂线上,只是要确定在平面![]() 的哪一侧,可分类讨论,同时由垂直得平行,从而得
的哪一侧,可分类讨论,同时由垂直得平行,从而得![]() 共线,求出外接球半径,求得
共线,求出外接球半径,求得![]() 后可得结论.
后可得结论.
如图,作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,由
,由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得
,得![]() ,同理
,同理![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() ,所以
,所以![]() ,
,
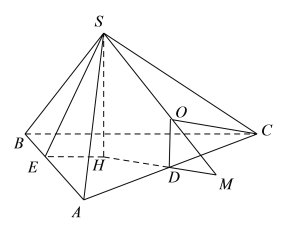
图1
又面角![]() 、
、![]() 、
、![]() 的大小均为
的大小均为![]() ,所以
,所以![]() 到
到![]() 三边距离相等,
三边距离相等,![]() 点到
点到![]() 的距离也相等,所以
的距离也相等,所以![]() 是
是![]() 的内心,
的内心,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,从而
,从而![]() ,
,![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
所以三棱锥![]() 的全面积为
的全面积为![]() ,
,
设内切球半径为![]() ,则
,则![]() ,所以
,所以![]() .
.
设![]() 是
是![]() 中点,则
中点,则![]() 是
是![]() 外心,所以
外心,所以![]() 平面
平面![]() ,所以
,所以![]() ,则
,则![]() 共线,
共线,
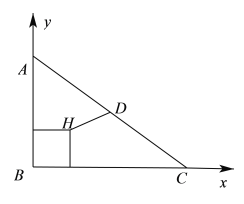
在直角![]() 中,以
中,以![]() 为
为![]() 轴建立平面直角坐标系,由
轴建立平面直角坐标系,由![]() ,
,![]() ,∴
,∴![]() ,
,
设三棱锥![]() 外接球半径为
外接球半径为![]() ,即
,即![]() ,若
,若![]() 在图1位置所示,由直角梯形
在图1位置所示,由直角梯形![]() 和直角
和直角![]() 得
得![]() (*),解得
(*),解得![]() 与(*)式不合,
与(*)式不合,
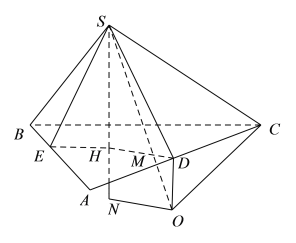
图2
若![]() 如图2位置所示,则
如图2位置所示,则![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
∴![]() ,∴
,∴![]() .
.
故答案为:![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】我国是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(Ⅱ)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱中ABC—A1B1C1,ABAC,AB=3,AC=4,B1CAC1.

(1)求AA1的长;
(2)试判断在侧棱BB1上是否存在点P,使得直线PC与平面AA1C1C所成角和二面角B—A1C—A的大小相等,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮).在相同的条件下,每轮甲乙两人站在同一位置上,甲先投,每人投一次篮,两人有![]() 人命中,命中者得
人命中,命中者得![]() 分,未命中者得
分,未命中者得![]() 分;两人都命中或都未命中,两人均得
分;两人都命中或都未命中,两人均得![]() 分.设甲每次投篮命中的概率为
分.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.
,且各次投篮互不影响.
(1)经过![]() 轮投篮,记甲的得分为
轮投篮,记甲的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
(2)若经过![]() 轮投篮,用
轮投篮,用![]() 表示第
表示第![]() 轮投篮后,甲的累计得分低于乙的累计得分的概率.
轮投篮后,甲的累计得分低于乙的累计得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机模拟计算可得
,经过计算机模拟计算可得![]() ,请根据①中
,请根据①中![]() 值求出
值求出![]() 的值,并由此求出数列
的值,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() ,
,![]() 、
、![]() 分別为
分別为![]() 、
、![]() 的中点
的中点![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
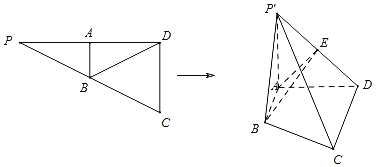
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,
的方向相同时,![]() 的正视图为直角三角形,求此时二面角
的正视图为直角三角形,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某中学理学社为了吸收更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参加.社团活动积极分子甲同学参加了活动.
①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.
②理学社设置了第![]() (
(![]() )个月中签的名额为
)个月中签的名额为![]() ,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参加,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第![]() (
(![]() )个月中签的概率为
)个月中签的概率为![]() ,活动进行了
,活动进行了![]() 个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于
个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于![]() 个月.
个月.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时,![]() 的面积为
的面积为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经点
经点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,设直线
,设直线![]() 过椭圆
过椭圆![]() 的上顶点和右焦点,坐标原点
的上顶点和右焦点,坐标原点![]() 到直线
到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 且斜率不为零的直线交椭圆
且斜率不为零的直线交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之积为非零的常数?若存在,求出定点
的斜率之积为非零的常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中总务处的老师要购买学校教学用的粉笔,并且有非常明确的判断一盒粉笔是“优质产品”和“非优质产品”的方法.某品牌的粉笔整箱出售,每箱共有20盒,根据以往的经验,其中会有某些盒的粉笔为非优质产品,其余的都为优质产品.并且每箱含有0,1,2盒非优质产品粉笔的概率为0.7,0.2和0.1.为了购买该品牌的粉笔,校总务主任设计了一种购买的方案:欲买一箱粉笔,随机查看该箱的4盒粉笔,如果没有非优质产品,则购买,否则不购买.设“买下所查看的一箱粉笔”为事件![]() ,“箱中有
,“箱中有![]() 件非优质产品”为事件
件非优质产品”为事件![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)随机查看该品牌粉笔某一箱中的四盒,设![]() 为非优质产品的盒数,求
为非优质产品的盒数,求![]() 的分布列及期望;
的分布列及期望;
(3)若购买100箱该品牌粉笔,如果按照主任所设计方案购买的粉笔中,箱中每盒粉笔都是优质产品的箱数的期望比随机购买的箱中每盒粉笔都是优质产品的箱数的期望大10,则所设计的方案有效.讨论该方案是否有效.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com