【题目】如图已知
，
，
、
分別为
、
的中点
，将
沿
折起，得到四棱锥
，
为
的中点.
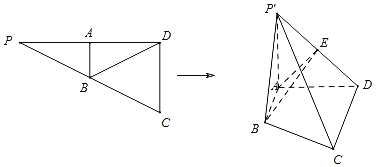
（1）证明：
平面
；
（2）当正视图方向与向量
的方向相同时，的正视图为直角三角形，求此时二面角
的余弦值.
【答案】（1）证明见解析；（2）
.
【解析】
（1）由平面图可知，
，
，得到
平面
，得
，再由已知可得
.由直线与平面垂直的判定可得
平面
；
（2）由
的正视图三角形与
全等，且为直角三角形，得
，以
为原点，分别以
、
、
所在直线为
、
、
轴建立空间直角坐标系，分别求出平面
的一个法向量与平面的一个法向量，由两法向量所成角的余弦值可得二面角
的余弦值.
（1）由平面图可知，，，
又
，
平面，
平面，
，
为
的中点，
，
.
，
平面；
（2）
四棱锥的正视图三角形与全等，且均为直角三角形，
，
以为原点，分别以、、所在直线为、、轴建立空间直角坐标系.
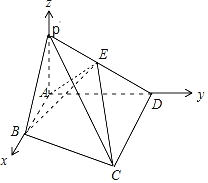
则
、
、
、
、
、
，
，
，
.
设平面的一个法向量为
，
由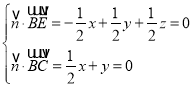
，取
，得
.
又
为平面的一个法向量，
设二面角为
，
.
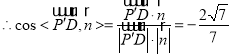由图形可知，二面角为钝角，所以，二面角的余弦值为.
科目：高中数学 来源： 题型：
【题目】如图，在长方体ABCD﹣HKLE中，底面ABCD是边长为3的正方形，对角线AC与BD相交于点O，点F在线段AH上且
，BE与底面ABCD所成角为
.
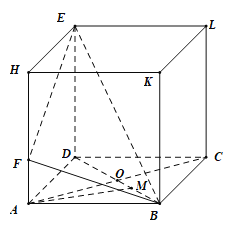
（1）求证：AC⊥BE；
（2）M为线段BD上一点，且
，求异面直线AM与BF所成角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
＝(cosx，sinx)，
＝(cosx，﹣sinx)，函数
．
（1）若
，x
(0，
)，求tan(x＋
)的值；
（2）若
，
(
，
)，
，
(0，)，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在
中，
分别为
的中点，
为
的一个三等分点（靠近点
）．将
沿
折起，记折起后点
为
，连接
为
上的一点，且
，连接
．
（1）求证：
平面
；
（2）若
，直线
与平面
所成的角为
，当最大时，求
，并计算
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥
中，
，二面角
、
、
的大小均为
，设三棱锥的外接球球心为
，直线
交平面
于点
，则三棱锥的内切球半径为_______________，
__________
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场推出消费抽现金活动，顾客消费满1000元可以参与一次抽奖，该活动设置了一等奖、二等奖、三等奖以及参与奖，奖金分别为：一等奖200元、二等奖100元、三等奖50元、参与奖20元，具体获奖人数比例分配如图，则下列说法中错误的是（ ）
A.获得参与奖的人数最多
B.各个奖项中一等奖的总金额最高
C.二等奖获奖人数是一等奖获奖人数的两倍
D.奖金平均数为
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
