
【题目】已知椭圆![]() :
:![]() ,长半轴长与短半轴长的差为
,长半轴长与短半轴长的差为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在![]() 轴上存在点
轴上存在点![]() ,过点
,过点![]() 的直线
的直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 为定值,求点
为定值,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() (2)
(2) 
【解析】
(1)由题意可得:a﹣b![]() ,
,![]() ,a2=b2+c2.联立解得:a,c,b.可得椭圆C的标准方程.
,a2=b2+c2.联立解得:a,c,b.可得椭圆C的标准方程.
(2)设M(t,0),P(x1,y1),Q(x2,y2).分类讨论:①当直线l的斜率不为0时,设直线l的方程为:x=my+t.与椭圆方程联立化为:(3m2+4)y2+6mty+3t2﹣12=0.△>0.可得|PM|2![]() (1+m2)
(1+m2)![]() ,同理可得:|PQ|2=(1+m2)
,同理可得:|PQ|2=(1+m2)![]() .把根与系数的关系代入
.把根与系数的关系代入 ,化简整理可得.②当直线l的斜率为0时,设P(2,0),Q(﹣2,0).|PM|=|t+2|,|QM|=|2﹣t|.代入同理可得结论.
,化简整理可得.②当直线l的斜率为0时,设P(2,0),Q(﹣2,0).|PM|=|t+2|,|QM|=|2﹣t|.代入同理可得结论.
(1)由题意可得:![]() ,
,![]() ,
,![]() .
.
联立解得:![]() ,
,![]() ,
,![]() ,∴椭圆
,∴椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2)设![]() ,
,![]() ,
,![]() .
.
①当直线![]() 的斜率不为0时,设直线
的斜率不为0时,设直线![]() 的方程为:
的方程为:![]() .
.
联立![]() ,化为:
,化为:![]() .
.![]() .
.
∴![]() ,
,![]() .
.
![]() ,同理可得:
,同理可得:![]() .
.
∴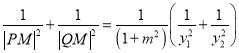
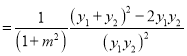
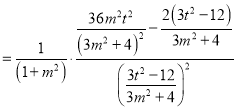
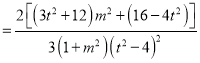 .
.
∵![]() 为定值,∴必然有
为定值,∴必然有![]() ,解得
,解得![]() .
.
此时![]() 为定值,
为定值, .
.
②当直线![]() 的斜率为0时,设
的斜率为0时,设![]() ,
,![]() .
.![]() ,
,![]() .
.
此时 ,把
,把![]() 代入可得:
代入可得:![]() 为定值.
为定值.
综上①②可得:![]() 为定值,
为定值, .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆长、短轴四个端点为顶点为四边形的面积为
,以椭圆长、短轴四个端点为顶点为四边形的面积为![]() .
.
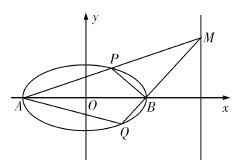
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图所示,记椭圆的左、右顶点分别为![]() 、
、![]() ,当动点
,当动点![]() 在定直线
在定直线![]() 上运动时,直线
上运动时,直线![]() 分别交椭圆于两点
分别交椭圆于两点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:
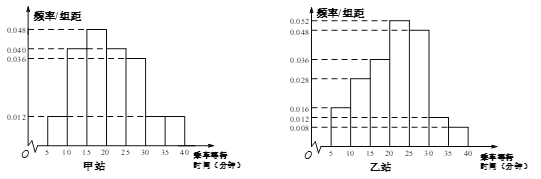
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为![]() ;从乙站的乘客中随机抽取1人,记为
;从乙站的乘客中随机抽取1人,记为![]() .用频率估计概率,求“乘客
.用频率估计概率,求“乘客![]() ,
,![]() 乘车等待时间都小于20分钟”的概率;
乘车等待时间都小于20分钟”的概率;
(2)从上班高峰时段,从乙站乘车的乘客中随机抽取3人,![]() 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量
表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点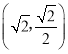 .
.
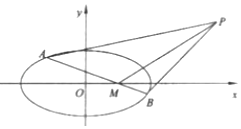
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交椭圆
的直线交椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
①若直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
②设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在定点
,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了200名用户,得到用户的满意度评分,现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
(1)求表格中的![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计用户的满意度评分的平均数;
(3)若从这200名用户中随机抽取50人,估计满意度评分高于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]() 、
、![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”.广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极鱼”.已知![]() 或
或 ,下列命题中:①
,下列命题中:①![]() 在平面直角坐标系中表示的区域的面积为
在平面直角坐标系中表示的区域的面积为![]() ;②
;②![]() ,使得
,使得![]() ;③
;③![]() ,都有
,都有![]() 成立;④设点
成立;④设点![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中真命题的个数为( )
.其中真命题的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com