
【题目】太极图被称为“中华第一图”.广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极鱼”.已知![]() 或
或 ,下列命题中:①
,下列命题中:①![]() 在平面直角坐标系中表示的区域的面积为
在平面直角坐标系中表示的区域的面积为![]() ;②
;②![]() ,使得
,使得![]() ;③
;③![]() ,都有
,都有![]() 成立;④设点
成立;④设点![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中真命题的个数为( )
.其中真命题的个数为( )

A.1B.2C.3D.4
【答案】B
【解析】
集合A表示的图形,分别分析选项,得到正确答案,
①根据图象,直接求判断集合A的面积是圆面积的一半;
②转化为两圆是否相交问题;
③设![]() ,
,![]() ,表示斜率为
,表示斜率为![]() 的直线,
的直线,![]() 表示纵截距,转化为线性规划问题;
表示纵截距,转化为线性规划问题;
④变形为![]() ,先求
,先求![]() 的范围,最后求
的范围,最后求![]() 的范围.
的范围.
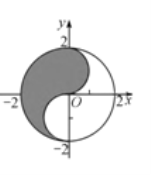
①如图,根据对称性可知,集合![]() 表示的面积占圆面积的一半,
表示的面积占圆面积的一半,![]() ,故①不正确;
,故①不正确;
②![]() ,整理为
,整理为![]() ,以
,以![]() 为圆心,
为圆心,![]() 的圆,与
的圆,与![]() 的圆的圆心距
的圆的圆心距![]() ,可知两圆相交,有2个交点,所以
,可知两圆相交,有2个交点,所以![]() ,使得
,使得![]() ,故②正确;
,故②正确;
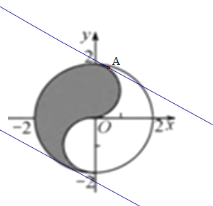
③设![]() ,
,![]() ,表示斜率为
,表示斜率为![]() 的直线,
的直线,![]() 表示纵截距,如图,当直线与圆
表示纵截距,如图,当直线与圆![]() 相切时,
相切时,![]() 取得最大值,此时圆心到直线的距离
取得最大值,此时圆心到直线的距离![]() ,解得
,解得![]() 或
或![]() ,如图,舍去
,如图,舍去![]() ,所以
,所以![]() 的最大值是
的最大值是![]() ,如图,当直线与
,如图,当直线与![]() 相切时,
相切时,![]() 取得最小值,圆心到直线的距离
取得最小值,圆心到直线的距离![]()
![]() ,
,![]() ,如图舍去
,如图舍去![]() ,所以
,所以![]() 的最小值是
的最小值是![]() ,所以
,所以![]() ,都有
,都有![]() 成立,③正确;
成立,③正确;
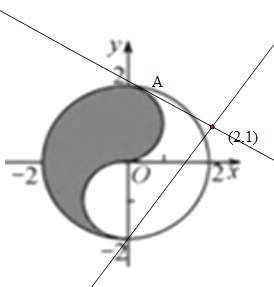
④![]() ,
,
设![]() 表示可行域内的点与点
表示可行域内的点与点![]() 连线的斜率,
连线的斜率,
设![]() ,当直线与圆
,当直线与圆![]() 相切时,圆心到直线的距离
相切时,圆心到直线的距离![]() ,解得
,解得![]() ,如图可知
,如图可知![]() ,
,
当直线过点![]() 时,斜率
时,斜率![]() ,其他满足条件的直线夹在这两直线之间,所以
,其他满足条件的直线夹在这两直线之间,所以![]() ,
,![]() ,
,![]() ,故④不正确.
,故④不正确.
故只有②③正确.
故选:B


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,长半轴长与短半轴长的差为
,长半轴长与短半轴长的差为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在![]() 轴上存在点
轴上存在点![]() ,过点
,过点![]() 的直线
的直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 为定值,求点
为定值,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某避暑山庄拟对一个半径为1百米的圆形地块(如图)进行改造,拟在该地块上修建一个等腰梯形![]() ,其中
,其中![]() ,
,![]() ,圆心
,圆心![]() 在梯形内部,设
在梯形内部,设![]() .当该游泳池的面积与周长之比最大时为“最佳游泳池”.
.当该游泳池的面积与周长之比最大时为“最佳游泳池”.

(1)求梯形游泳池的面积![]() 关于
关于![]() 的函数关系式,并指明定义域;
的函数关系式,并指明定义域;
(2)求当该游泳池为“最佳游泳池”时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租用一个门店作展馆,准备对其公司生产的某型产品进行为期一年的展出。为此,需对门店进行装修,展出结束,门店不再使用,现市面上有某品牌的![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过
型节能灯使用寿命都超过![]() 小时,经销商对
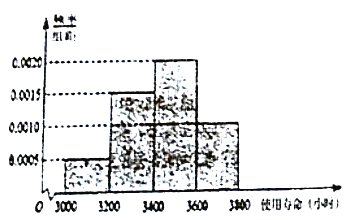
小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
门店装修时,需安装该品牌节能灯![]() 支(同种型号).经了解,
支(同种型号).经了解,![]() 型
型![]() 瓦和B型
瓦和B型![]() 瓦的两种节能灯照明效果相当,都适合安装。已知
瓦的两种节能灯照明效果相当,都适合安装。已知![]() 型和
型和![]() 型节能灯每支的价格分别为
型节能灯每支的价格分别为![]() 元、
元、![]() 元,当地商业电价为
元,当地商业电价为![]() 元/千瓦时。假定该店面一年周转期的照明时间为
元/千瓦时。假定该店面一年周转期的照明时间为![]() 小时,若正常营业期间灯坏了立即购买同型灯管更换。(用频率估计概率)
小时,若正常营业期间灯坏了立即购买同型灯管更换。(用频率估计概率)
(1)根据频率直方图估算B型节能灯的平均使用寿命;
(2)根据统计知识,若一支灯管一年内需要更换的概率为![]() ,那么支灯管一年内估计需要更换
,那么支灯管一年内估计需要更换![]() 支.若该商家新店面全部安装
支.若该商家新店面全部安装![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(3)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年的政府工作报告强调,要树立绿水青山就是金山银山理念,以前所未有的决心和力度加强生态环境保护.某地科技园积极检查督导园区内企业的环保落实情况,并计划采取激励措施引导企业主动落实环保措施,下图给出的是甲、乙两企业2012年至2017年在环保方面投入金额(单位:万元)的柱状图.
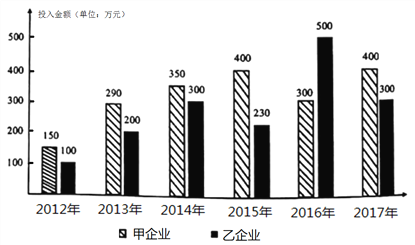
(Ⅰ)分别求出甲、乙两企业这六年在环保方面投入金额的平均数;(结果保留整数)
(Ⅱ)园区管委会为尽快落实环保措施,计划对企业进行一定的奖励,提出了如下方案:若企业一年的环保投入金额不超过200万元,则该年不奖励;若企业一年的环保投入金额超过200万元,不超过300万元,则该年奖励20万元;若企业一年的环保投入金额超过300万元,则该年奖励50万元.
(ⅰ)分别求出甲、乙两企业这六年获得的奖励之和;
(ⅱ)现从甲企业这六年中任取两年对其环保情况作进一步调查,求这两年获得的奖励之和不低于70万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年的政府工作报告强调,要树立绿水青山就是金山银山理念,以前所未有的决心和力度加强生态环境保护.某地科技园积极检查督导园区内企业的环保落实情况,并计划采取激励措施引导企业主动落实环保措施,下图给出的是甲、乙两企业2012年至2017年在环保方面投入金额(单位:万元)的柱状图.
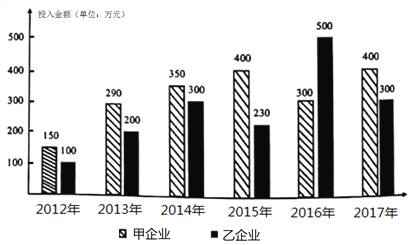
(Ⅰ)分别求出甲、乙两企业这六年在环保方面投入金额的平均数;(结果保留整数)
(Ⅱ)园区管委会为尽快落实环保措施,计划对企业进行一定的奖励,提出了如下方案:若企业一年的环保投入金额不超过200万元,则该年不奖励;若企业一年的环保投入金额超过200万元,不超过300万元,则该年奖励20万元;若企业一年的环保投入金额超过300万元,则该年奖励50万元.
(ⅰ)分别求出甲、乙两企业这六年获得的奖励之和;
(ⅱ)现从甲企业这六年中任取两年对其环保情况作进一步调查,求这两年获得的奖励之和不低于70万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(Ⅰ)当![]() ,且直线
,且直线![]()
![]() 轴时, 求四边形
轴时, 求四边形![]() 的面积;
的面积;
(Ⅱ)设![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com