
【题目】如图所示,在四棱锥S—ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,其中AB∥CD,∠ADC=90°,AD=AS=2,AB=1,CD=3,点E在棱CS上,且CE=λCS.
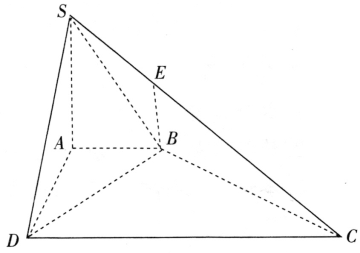
(1)若![]() ,证明:BE⊥CD;
,证明:BE⊥CD;
(2)若![]() ,求点E到平面SBD的距离.
,求点E到平面SBD的距离.
【答案】(1)见解析;(2)点E到平面SBD的距离为![]() .
.
【解析】
(1)在线段![]() 上取一点
上取一点![]() 使
使![]() ,连接
,连接![]() , 可得
, 可得![]() 垂直
垂直![]() .再证明
.再证明![]() 垂直平面
垂直平面![]() ,所以
,所以![]() 垂直
垂直![]() ,又
,又![]() 垂直
垂直![]() .由此得
.由此得![]() 垂直平面
垂直平面![]() ,从而可得结果;(2)先求得
,从而可得结果;(2)先求得![]() ,再求得
,再求得![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() 得
得![]() ,从而可得结果.
,从而可得结果.
(1)因为![]() ,所以
,所以![]() ,在线段CD上取一点F使
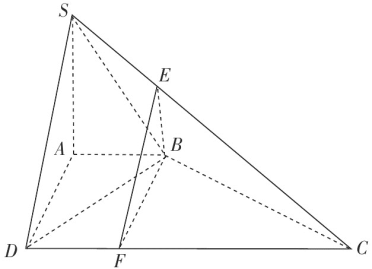
,在线段CD上取一点F使![]() ,连接EF,BF,则EF∥SD且DF=1.
,连接EF,BF,则EF∥SD且DF=1.
因为AB=1,AB∥CD,∠ADC=90°,
所以四边形ABFD为矩形,所以CD⊥BF.
又SA⊥平面ABCD,∠ADC=90°,
所以SA⊥CD,AD⊥CD.
因为AD∩SA=A,所以CD⊥平面SAD,
所以CD⊥SD,从而CD⊥EF.
因为BF∩EF=F,所以CD⊥平面BEF.
又BE![]() 平面BEF,所以CD⊥BE.
平面BEF,所以CD⊥BE.
(2)解:
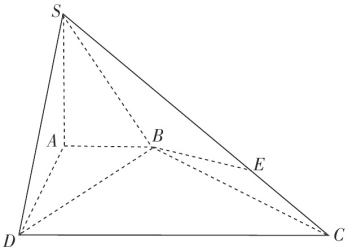
由题设得,![]() ,
,
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
设点C到平面SBD的距离为h,则由VS—BCD=VC—SBD得![]() ,
,
因为![]() ,所以点E到平面SBD的距离为
,所以点E到平面SBD的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论中错误的是 ( )

A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,有下列结论:
中,有下列结论:
①![]() 平面
平面![]() ;
;
②异面直线AD与![]() 所成的角为
所成的角为![]() ;
;
③三棱柱![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的四倍;
的体积的四倍;
④在四面体![]() 中,分别连接三组对棱的中点的线段互相垂直平分.
中,分别连接三组对棱的中点的线段互相垂直平分.
其中正确的是________(填出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
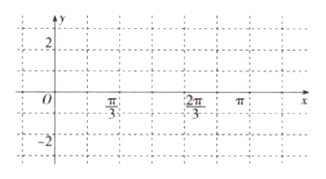
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
(1)请将上表数据补充完整,并写出函数![]() 的解析式(直接写出结果即可);
的解析式(直接写出结果即可);
(2)根据表格中的数据作出![]() 在一个周期内的图像;
在一个周期内的图像;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 的动点,设直线
的动点,设直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,直线
的交线,直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,下列结论中错误的是( )
的交线,下列结论中错误的是( )

A.![]() 平面
平面![]() B.平面
B.平面![]() 与平面
与平面![]() 不垂直
不垂直
C.平面![]() 与平面
与平面![]() 可能平行D.直线
可能平行D.直线![]() 与直线
与直线![]() 可能不平行
可能不平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com