Question

【题目】网购是当前民众购物的新方式，某公司为改进营销方式，随机调査了100名市民，统计其周平均网购

的次数，并整理得到如右的频数直方图，将周平均网购次数不小于4次的民众称为网购迷．这100名市民中，年龄不超过40岁的有65人，且网购迷中有5名市民的年龄超过40岁

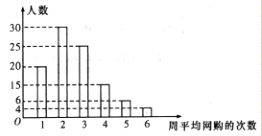
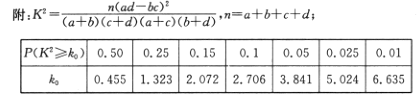
（1）根据已知条件完成下面的2×2列联表，能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关？

（2）现从网购迷中按分层抽样选5人代表进一步进行调查，若从5人代表中任意挑选2人，求挑选的2人中有年龄超过40岁的概率

Answer 1

【答案】（1）见解析；（2）

【解析】

(1)根据已知条件中的数据填写列联表，由公式计算，然后与表格中的临界值比较可得结论；（2）由列举法得到基本事件总数，然后由古典概型的概率公式计算即可.

（1）根据已知条件完成2×2列联表，如下：

	网购迷	非网购迷	合计
年龄不超过40岁	20	45	65
年龄超过40岁	5	30	35
合计	25	75	100

计算，

因为3.297>2.706，

所以据此列联表判断，能在犯错误的概率不超过0.10的前提下，认为网购迷与年龄不超过40岁有关.

（2）由频数分布直方图知，网购迷共有25人，现从网购迷中按分层抽样选5人代表，记其中年龄超过40岁的1名市民为，其余4名年龄不超过40岁的市民为，现从5人中任取2人，基本事件是共有10种，

其中有市民年龄超过40岁的基本事件是共4种，

故所求的概率为，.