
【题目】![]() 为何值时,方程组
为何值时,方程组![]()
(1)有一个实数解,并求出方程组的解集;
(2)有两个不相等的实数解;
(3)没有实数解.
【答案】(1)k=0,方程组的解为![]() ;k=1,方程组的解为
;k=1,方程组的解为![]() ;(2)k<1且k≠0;(3)k>1
;(2)k<1且k≠0;(3)k>1
【解析】
先利用代入消元法得到![]() ,
,
(1)分类讨论:当k=0,易得y=2,且方程化为一次方程,解得![]() ,于是得到原方程组的一组解;当k≠0,方程为一元二次方程,若
,于是得到原方程组的一组解;当k≠0,方程为一元二次方程,若![]() ,方程有两个相等的实数解,而对于方程组来说,只有一组实数解,然后计算出k=1,再分别求出x和y的值,得到原方程组的一组解;
,方程有两个相等的实数解,而对于方程组来说,只有一组实数解,然后计算出k=1,再分别求出x和y的值,得到原方程组的一组解;
(2)当![]() 有两个不相等的实数解时,方程组有两组实数解,则k≠0,
有两个不相等的实数解时,方程组有两组实数解,则k≠0,![]() ,然后求出k的范围;
,然后求出k的范围;
(3)当![]() 没有实数解时,方程组没有实数解,则k≠0,
没有实数解时,方程组没有实数解,则k≠0,![]() ,然后求出k的范围.
,然后求出k的范围.
解:把![]() 代入
代入![]() 得
得![]() ,
,
整理得![]() ,
,
(1)当k=0,则![]() ,解得
,解得![]() ,
,
方程组的解为![]() ;
;
当k≠0,![]() ,解得k=1,
,解得k=1,
方程化为![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以方程组的解为![]() ;
;
(2)当k≠0,![]() ,解得k<1,
,解得k<1,
所以当k<1且k≠0时,方程组有两个实数解;
(3)当k≠0,![]() ,解得k>1,
,解得k>1,
所以当k>1时,方程组没有实数解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
:  (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
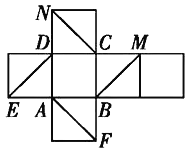
【题目】如图所示是一个正方体的平面展开图,在这个正方体中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四个命题中,真命题的序号是
平面NCF.以上四个命题中,真命题的序号是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
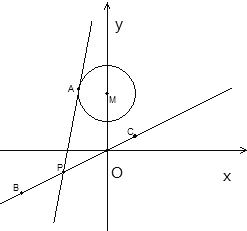
【题目】已知圆M:![]() ,设点B,C是直线l:
,设点B,C是直线l:![]() 上的两点,它们的横坐标分别是t,
上的两点,它们的横坐标分别是t,![]() ,P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
,P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
![]() 若
若![]() ,
,![]() ,求直线PA的方程;
,求直线PA的方程;
![]() 经过A,P,M三点的圆的圆心是D,
经过A,P,M三点的圆的圆心是D,
![]() 将
将![]() 表示成a的函数
表示成a的函数![]() ,并写出定义域.
,并写出定义域.
![]() 求线段DO长的最小值.
求线段DO长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长为2.直线l:y=kx+m与椭圆C交于M,N两点,又l与直线
,短轴长为2.直线l:y=kx+m与椭圆C交于M,N两点,又l与直线![]() ,
, ![]() 分别交于A,B两点,其中点A在第一象限,点B在第二象限,且△OAB的面积为2(O为坐标原点).
分别交于A,B两点,其中点A在第一象限,点B在第二象限,且△OAB的面积为2(O为坐标原点).
(1)求椭圆C的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足an=2an-1+2n+1(n∈N*,n≥2),
满足an=2an-1+2n+1(n∈N*,n≥2), ![]() .
.
(1)求![]() 的值;
的值;
(2)是否存在一个实数t,使得![]() (n∈N*),且数列{
(n∈N*),且数列{![]() }为等差数列?若存在,求出实数t;若不存在,请说明理由;
}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
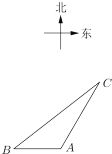
【题目】如图,一智能扫地机器人在![]() 处发现位于它正西方向的
处发现位于它正西方向的![]() 处和北偏东30°方向上的
处和北偏东30°方向上的![]() 处分别有需要清扫的垃圾,红外线感应测量发现机器人到
处分别有需要清扫的垃圾,红外线感应测量发现机器人到![]() 的距离比到
的距离比到![]() 的距离少0.4米,于是选择沿
的距离少0.4米,于是选择沿![]() 路线清扫,已知智能扫地机器人的直线行走速度为0.2
路线清扫,已知智能扫地机器人的直线行走速度为0.2![]() ,忽略机器人吸入垃圾及在
,忽略机器人吸入垃圾及在![]() 处旋转所用时间,10秒钟完成了清扫任务.
处旋转所用时间,10秒钟完成了清扫任务.
(1)![]() 、
、![]() 两处垃圾的距离是多少?
两处垃圾的距离是多少?
(2)智能扫地机器人此次清扫行走路线的夹角![]() 的正弦值是多少?
的正弦值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com