
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且关于
,且关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析.
(2)![]() .
.
【解析】
(1)确定函数定义域并求出导数![]() ,令
,令![]() ,得导数
,得导数![]() 的零点,根据导数
的零点,根据导数![]() 的两零点的与定义域的位置关系,分类讨论函数的单调区间,即可得出答案;
的两零点的与定义域的位置关系,分类讨论函数的单调区间,即可得出答案;
(2)构造新函数![]() ,分两类情况讨论:①当
,分两类情况讨论:①当![]() 时符合题意;②当
时符合题意;②当![]() 时对函数
时对函数![]() 求导,确定其在定义域范围最小值
求导,确定其在定义域范围最小值![]()
![]() ,又将
,又将![]() 恒成立,化简为
恒成立,化简为![]() 恒成立,根据
恒成立,根据![]() 的单调性,确定最小值
的单调性,确定最小值![]() ;由
;由![]() 得
得![]() ,令函数
,令函数![]() ,根据其在区间
,根据其在区间![]() 的单调性确定
的单调性确定![]() 的范围;综合两种情况即可得出实数
的范围;综合两种情况即可得出实数![]() 的取值范围.
的取值范围.
解:(1)![]() ,定义域
,定义域![]() ,
,
![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() .
.
①当![]() ,
,![]() 即
即![]() 时,
时,![]() 在
在![]() 递减,
递减,![]() 递增.
递增.
②当![]() ,
,![]() 即
即![]() 时,
时,![]() 在
在![]() 递增,
递增,![]() 递减,
递减,![]() 递增.
递增.
综上,当![]() 时,
时,![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() ,
,
当![]() 时,
时,![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() ,
,![]() .
.
(2)由题意![]() ,令
,令![]() 定义域
定义域![]() ,
,
①当![]() 时,
时,![]() 符合题意,
符合题意,
②当![]() 时,
时,![]() ,令
,令![]() .
.
∵![]() ,∴
,∴![]() ,则该方程有两不同实根,且一正一负,
,则该方程有两不同实根,且一正一负,
即存在![]() ,使得
,使得![]() ,
,
可知![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() 恒成立
恒成立 ![]() ,即
,即![]() ,
,
∵![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 单调递减,
单调递减,
∴![]() 即为
即为![]() 的范围.
的范围.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为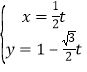 (t为参数
(t为参数![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为
以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 判断直线l与圆C的交点个数;
判断直线l与圆C的交点个数;
![]() Ⅱ
Ⅱ![]() 若圆C与直线l交于A,B两点,求线段AB的长度.
若圆C与直线l交于A,B两点,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知t为实数,函数![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(2)当![]() 时,
时,![]() 的图象始终在
的图象始终在![]() 的图象的下方,求t的取值范围;
的图象的下方,求t的取值范围;
(3)设![]() ,当
,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com