
【题目】给出下列说法:①方程![]() 表示的图形是一个点;②命题“若
表示的图形是一个点;②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;③已知双曲线
”为真命题;③已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 被双曲线截得的弦长为4的直线有3条;④已知椭圆
被双曲线截得的弦长为4的直线有3条;④已知椭圆![]() :
:![]()
![]() 上有两点
上有两点![]() ,
,![]() ,若点
,若点![]() 是椭圆
是椭圆![]() 上任意一点,且
上任意一点,且![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() ;⑤已知命题“
;⑤已知命题“![]() ,
,![]() 满足
满足![]() ,
,![]() ”是真命题,则实数
”是真命题,则实数![]() .其中说法正确的序号是__________.
.其中说法正确的序号是__________.
【答案】①②④
【解析】
利用曲线与方程可判定①是正确;根据四种命题的关系,可得②是正确的;根据双曲线的几何性质,可得③是不正确的;根据直线与椭圆的位置关系,可判定④是正确的;直线与圆的位置关系,可判定⑤是不正确的,得到答案.
对于①中,由方程![]() ,可得
,可得![]() ,解得
,解得![]() ,即方程表示的图形是一个点
,即方程表示的图形是一个点![]() ,所以是正确的;
,所以是正确的;
对于②中,根据四种命题的定义,可得命题“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为“若
”的逆否命题为“若![]() 且
且![]() ,则
,则![]() ”为真,所以原命题为真,所以是正确的;
”为真,所以原命题为真,所以是正确的;
对于③中,根据双曲线的性质,可得两支总实轴最短,最短为![]() ,同支焦点弦通径最短,最短为
,同支焦点弦通径最短,最短为![]() ,所以满足条件的直线只有2条,所以不正确;
,所以满足条件的直线只有2条,所以不正确;
对于④中,由已知可得![]() ,
,
又由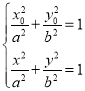 相减可得
相减可得![]() ,
,
则![]() ,所以是正确的;
,所以是正确的;
对于⑤中,令![]() ,即
,即![]() ,数形结合,如图所示,
,数形结合,如图所示,
圆心到直线的距离我![]() ,解得
,解得![]() ,
,
又由由已知可得![]() 存在成立,则
存在成立,则![]() ,所以不正确.
,所以不正确.
综上可得:正确命题的序号为:①②④.
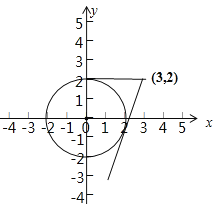


科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
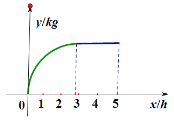
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() (
(![]() ).
).
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 满足:
满足:![]() ,
,![]() .
.
① 求数列![]() 的通项公式;
的通项公式;
② 是否存在正整数n,使得![]() 成立?若存在,求出所有n的值;若不存在,请说明理由.
成立?若存在,求出所有n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机场建在一个海湾的半岛上,飞机跑道![]() 的长为
的长为![]() ,且跑道所在的直线与海岸线l的夹角为
,且跑道所在的直线与海岸线l的夹角为![]() (海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离
(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离![]() .D为海湾一侧海岸线
.D为海湾一侧海岸线![]() 上的一点,设
上的一点,设![]() (
(![]() ),点D对跑道
),点D对跑道![]() 的视角为
的视角为![]() .
.

(1)将![]() 表示为x的函数;
表示为x的函数;
(2)求点D的位置,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com