
【题目】已知圆![]() 经过
经过![]() ,
,![]() 两点,且圆心在直线
两点,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)从![]() 轴上一个动点
轴上一个动点![]() 向圆
向圆![]() 作切线,求切线长的最小值及对应切线方程.
作切线,求切线长的最小值及对应切线方程.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)设圆![]() 的方程为
的方程为![]() ,根据题设条件,列出方程组,求得
,根据题设条件,列出方程组,求得![]() 的值,即可求得圆的方程;
的值,即可求得圆的方程;
(2)利用圆的切线长公式![]() ,结合直线与圆的位置关系,分类讨论,即可求解.
,结合直线与圆的位置关系,分类讨论,即可求解.
(1)设圆![]() 的方程为
的方程为![]() ,
,
由圆![]() 经过
经过![]() ,
,![]() 两点,
两点,
可得![]() , ……①
, ……① ![]() ,……②
,……②
又由圆心![]() 在直线
在直线![]() 上,即
上,即![]() ,……③
,……③
由①②③,可解得![]() ,
,![]() ,
,![]() ,
,
所以圆![]() 的方程为:
的方程为:![]() ,
,
即圆![]() 的方程
的方程![]() .
.
(2)对于动点![]() ,设切线长为
,设切线长为![]() ,则
,则![]() ,
,
所以要使得切线长最短,必须且只需![]() 最小即可,
最小即可,
最小值为圆心![]() 到
到![]() 轴的距离,此时距离为2,
轴的距离,此时距离为2,
故切线长的最小值为![]() ,当切线长取最小值时,对应
,当切线长取最小值时,对应![]() 点为原点,
点为原点,
过原点的直线中,当斜率不存在时,不与圆![]() 相切;
相切;
当斜率存在时,设直线方程为![]() ,
,
代入圆![]() :
:![]() ,可得
,可得![]() ,即
,即![]() ,
,
令![]() ,解得
,解得![]() ,
,
故切线方程为![]() ,此时切线长为
,此时切线长为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形.
是菱形.
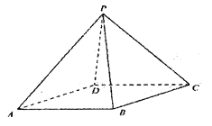
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,若
上的点,若![]() 平面
平面![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,判断
,判断![]() 是否为等腰三角形?并说明理由.
是否为等腰三角形?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①方程![]() 表示的图形是一个点;②命题“若
表示的图形是一个点;②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;③已知双曲线
”为真命题;③已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 被双曲线截得的弦长为4的直线有3条;④已知椭圆
被双曲线截得的弦长为4的直线有3条;④已知椭圆![]() :
:![]()
![]() 上有两点
上有两点![]() ,
,![]() ,若点
,若点![]() 是椭圆
是椭圆![]() 上任意一点,且
上任意一点,且![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() ;⑤已知命题“
;⑤已知命题“![]() ,
,![]() 满足
满足![]() ,
,![]() ”是真命题,则实数
”是真命题,则实数![]() .其中说法正确的序号是__________.
.其中说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:
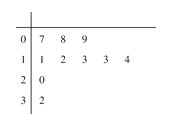
(Ⅰ)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数X的分布列与数学期望;
(Ⅱ)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为一阶的可能性最大,求
户月用水量为一阶的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com