
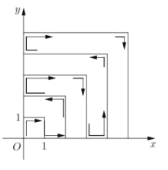
【题目】如图,一个粒子从原点出发,在第一象限和两坐标轴正半轴上运动,在第一秒时它从原点运动到点![]() ,接着它按图所示在
,接着它按图所示在![]() 轴、
轴、![]() 轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
【答案】![]()
【解析】
分析粒子在第一象限的运动规律得到数列{an}通项的递推关系式an-an-1=2n,利用累加法求出an=n(n+1),由44×45=1980知,运动了1980秒时粒子到点A44(44,44),对运动规律的探索知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动,由此可求得结果.
如图,设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,
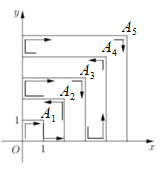
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
将a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n相加得:an-a1=2(2+3+4+…+n)=n2+n-2,则an=n(n+1),由44×45=1980,故运动了1980秒时它到点A44(44,44),
又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动,
故粒子到达A44(44,44)时向左运动38秒即运动了2018秒到达点(6,44),
则所求点应为(6,44).
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,求证:直线
的垂直平分线,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
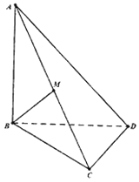
(1)若![]() 中点是
中点是![]() ,求证:
,求证:![]() 面
面![]() ;
;
(2)若![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 是面
是面![]() 上的动点,且线段
上的动点,且线段![]() ,
,![]() 的中点是
的中点是![]() ,求动点
,求动点![]() 的轨迹与四面体
的轨迹与四面体![]() 围成的较小的几何体的体积.
围成的较小的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在所有棱长都相等的三棱锥![]() 中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正确命题的序号为________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() )时,每小时的油耗(所需要的汽油量)为
)时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以![]() 千米/小时的速度行驶时,每小时的油耗为
千米/小时的速度行驶时,每小时的油耗为![]() 升,欲使每小时的油耗不超过
升,欲使每小时的油耗不超过![]() 升,求
升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶![]() 千米的油耗的最小值.
千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B为椭圆![]() (
(![]() )和双曲线
)和双曲线![]() 的公共顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且
的公共顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且![]() (
(![]() ,
,![]() ),设AP、BP、AQ、BQ的斜率分别为
),设AP、BP、AQ、BQ的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若![]() ,求
,求![]() 的值(用a、b的代数式表示);
的值(用a、b的代数式表示);
(2)求证:![]() ;
;
(3)设![]() 、
、![]() 分别为椭圆和双曲线的右焦点,若
分别为椭圆和双曲线的右焦点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江苏省滨临黄海,每年夏秋季节常常受到台风的侵袭.据监测,台风![]() 生成于西北太平洋洋面上,其中心位于
生成于西北太平洋洋面上,其中心位于![]() 市南偏东
市南偏东![]() 方向的
方向的![]() 处,该台风先沿北偏西
处,该台风先沿北偏西![]() 方向移动
方向移动![]() 后在
后在![]() 处登陆,登陆点
处登陆,登陆点![]() 在
在![]() 市南偏东
市南偏东![]() 方向
方向![]() 处,之后,台风
处,之后,台风![]() 将以
将以![]() 的速度沿北偏西
的速度沿北偏西![]() 方向继续移动.已知登陆时台风
方向继续移动.已知登陆时台风![]() 的侵袭范围(圆形区域)半径为
的侵袭范围(圆形区域)半径为![]() ,并以
,并以![]() 的速度不断增大.(
的速度不断增大.(![]() )
)
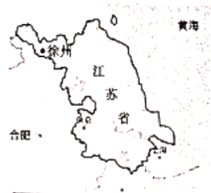
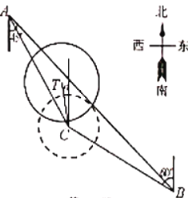
(1)求台风![]() 生成时中心
生成时中心![]() 与
与![]() 市的距离;
市的距离;
(2)台风![]() 登陆后多少小时开始侵袭
登陆后多少小时开始侵袭![]() 市?(保留两位有效数字)
市?(保留两位有效数字)
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,过点
的长轴长为4,过点![]() 且斜率为
且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点
的中点
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 为坐标原点,过右焦点
为坐标原点,过右焦点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,(
两点,(![]() 不在
不在![]() 轴上),求
轴上),求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点至少有一个在原点右侧.
轴的交点至少有一个在原点右侧.
(1)求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,求
,求![]() 的值(其中
的值(其中![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() );
);
(3)对(2)中的![]() 求函数
求函数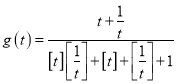 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com