
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,求证:直线
的垂直平分线,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]() ,详见解析.
,详见解析.
【解析】
(1)由焦点和离心率可得![]() 的值,则方程易求.
的值,则方程易求.
(2)设出直线![]() 的方程,与椭圆方程联立,结合线段的中点,利用根与系数的关系(或点差法)可求出直线
的方程,与椭圆方程联立,结合线段的中点,利用根与系数的关系(或点差法)可求出直线![]() 的斜率,进而可表示出直线
的斜率,进而可表示出直线![]() 的方程,判断其所过定点.
的方程,判断其所过定点.
(1)抛物线![]() 的焦点为
的焦点为![]() ,则
,则![]() .
.
椭圆![]() 的离心率
的离心率![]() ,则
,则![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)方法一:显然点![]() 在椭圆
在椭圆![]() 内部,故
内部,故![]() ,且直线
,且直线![]() 的斜率不为
的斜率不为![]() .
.
当直线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,易知
时,易知![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程并化简得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,解得
,解得![]() .
.
因为直线![]() 是线段
是线段![]() 的垂直平分线,故直线
的垂直平分线,故直线![]() ,即
,即![]() .
.
令![]() ,此时
,此时![]() ,于是直线
,于是直线![]() 过定点
过定点![]() .
.
当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() ,此时直线
,此时直线![]() ,故直线
,故直线![]() 过定点
过定点![]() .
.
综上所述,直线![]() 过定点
过定点![]() .
.
方法二:显然点![]() 在椭圆
在椭圆![]() 内部,故
内部,故![]() ,且直线
,且直线![]() 的斜率不为
的斜率不为![]() .
.
当直线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设
时,设![]() ,
,![]() ,
,
则有![]() ,
,![]() ,
,
两式相减得![]() .
.
由线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
故直线![]() 的斜率
的斜率![]() .
.
因为直线![]() 是线段
是线段![]() 的垂直平分线,故直线
的垂直平分线,故直线![]() ,即
,即![]() .
.
令![]() ,此时
,此时![]() ,于是直线
,于是直线![]() 过定点
过定点![]() .
.
当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() ,此时直线
,此时直线![]() ,故直线
,故直线![]() 过定点
过定点![]() .
.
综上所述,直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学小组到进行社会实践调查,了解鑫鑫桶装水经营部在为如何定价发愁。进一步调研了解到如下信息:该经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表:
销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
根据以上信息,你认为该经营部定价为多少才能获得最大利润?( )
A.每桶8.5元B.每桶9.5元C.每桶10.5元D.每桶11.5元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击小组有甲、乙、丙三名射手,已知甲击中目标的概率是![]() ,甲、丙二人都没有击中目标的概率是
,甲、丙二人都没有击中目标的概率是![]() ,乙、丙二人都击中目标的概率是
,乙、丙二人都击中目标的概率是![]() .甲乙丙是否击中目标相互独立.
.甲乙丙是否击中目标相互独立.
(1)求乙、丙二人各自击中目标的概率;
(2)设乙、丙二人中击中目标的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,点
上任意一点,点![]() 关于原点
关于原点![]() 的对称点为点
的对称点为点![]() ,有
,有![]() ,且当
,且当![]() 的面积最大时为等边三角形.
的面积最大时为等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)与圆![]() 相切的直线
相切的直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,若椭圆上存在点
两点,若椭圆上存在点![]() 满足
满足![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
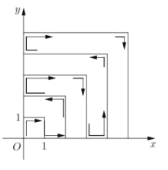
【题目】如图,一个粒子从原点出发,在第一象限和两坐标轴正半轴上运动,在第一秒时它从原点运动到点![]() ,接着它按图所示在
,接着它按图所示在![]() 轴、
轴、![]() 轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com