
【题目】如图,在平行六面体![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 与底面
与底面![]() 所成角为
所成角为![]() ,
,![]() .
.
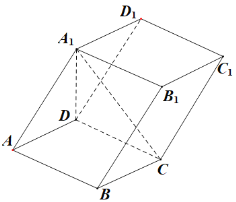
(1)求证:平行六面体![]() 的体积
的体积![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)若![]() ,求二面角
,求二面角![]() 所成角的大小.
所成角的大小.
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() 如下:对于实数
如下:对于实数![]() ,如果存在整数
,如果存在整数![]() ,使得
,使得![]() ,则
,则![]() .则下列结论:①
.则下列结论:①![]() 是实数
是实数![]() 上的递增函数;②
上的递增函数;②![]() 是周期为1的函数;③
是周期为1的函数;③![]() 是奇函数;④函数
是奇函数;④函数![]() 的图像与直线
的图像与直线![]() 有且仅有一个交点.则正确结论的序号是______.
有且仅有一个交点.则正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
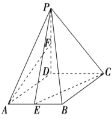
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
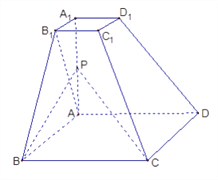
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形
中,底面四边形![]() 为正方形,已知
为正方形,已知![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
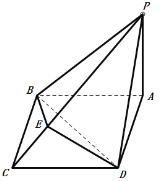
(1)证明:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值并证明,若不存在,说明理由.
的值并证明,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(I)求Z的分布列和均值;
(II)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com