
【题目】如图,四棱锥PABCD的底面为正方形,PD底面ABCD.设平面PAD与平面PBC的交线为![]() .
.
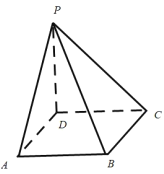
(1)证明:![]() 平面PDC;
平面PDC;
(2)已知PDAD1,Q为![]() 上的点,QB=
上的点,QB=![]() ,求PB与平面QCD所成角的正弦值.
,求PB与平面QCD所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用线面平行的判定定理以及性质定理,证得![]() ,利用线面垂直的判定定理证得
,利用线面垂直的判定定理证得![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() ;
;
(2)根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点![]() ,之后求得平面
,之后求得平面![]() 的法向量以及向量
的法向量以及向量![]() 的坐标,求得
的坐标,求得![]() ,即可得到直线
,即可得到直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:
在正方形![]() 中,
中,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,
,
因为在四棱锥![]() 中,底面
中,底面![]() 是正方形,所以
是正方形,所以![]()
且![]() 平面
平面![]() ,所以
,所以![]()
因为![]()
所以![]() 平面
平面![]() ;
;
(2)如图建立空间直角坐标系![]() ,
,
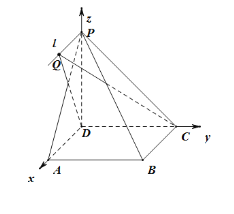
因为![]() ,则有
,则有![]() ,
,
设![]() ,则有
,则有![]() ,
,
因为QB=![]() ,所以有
,所以有![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则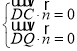 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
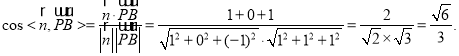
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 经过坐标原点
经过坐标原点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以点
为参数).以点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与
与![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() 、
、![]() ,且
,且![]() ,求
,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“L函数”.
为“L函数”.
(1)试判断函数![]() 与
与![]() 是否是“L函数”;
是否是“L函数”;
(2)若函数![]() 为“L函数”,求实数a的取值范围;
为“L函数”,求实数a的取值范围;
(3)若函数![]() 为“L函数”,且
为“L函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的定义域
的定义域![]() 恰是不等式
恰是不等式![]() 的解集,其值域为
的解集,其值域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(1)求![]() 定义域
定义域![]() 和值域
和值域![]() ;
;
(2)试用单调性的定义法解决问题:若存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围并用
的取值范围并用![]() 表示
表示![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com