
【题目】已知曲线![]() 的极坐标程是
的极坐标程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程
的参数方程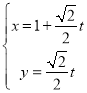 ,(
,(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为曲线
为曲线![]() 上的动点,求三角形
上的动点,求三角形![]() 面积的最大值.
面积的最大值.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
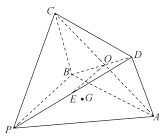
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为平面
为平面![]() 内任一点.
内任一点.
(1)在平面![]() 内,过
内,过![]() 点是否存在直线
点是否存在直线![]() 使
使![]() ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;
(2)过![]() ,
, ![]() ,
, ![]() 三点的平面将几何体
三点的平面将几何体![]() 截去三棱锥
截去三棱锥![]() ,求剩余几何体
,求剩余几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示,该基地周光照量![]() (小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量![]() (千克)与使用某种液体肥料的质量
(千克)与使用某种液体肥料的质量![]() (千克)之间的关系如图所示.
(千克)之间的关系如图所示.
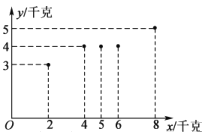
(1)依据上图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以频率作为概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式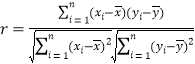 ,
,
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四面体![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中点,且
的中点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年高考总成绩由语数外三门统考科目和物理、化学等六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩![]() 大致服从正态分布
大致服从正态分布![]() .
.
(1)求该市化学原始成绩在区间![]() 的人数;
的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间![]() 的人数,求
的人数,求![]() .
.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线l的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数).
为参数).
![]() 若曲线上存在M,N两点关于直线l对称,求实数m的值;
若曲线上存在M,N两点关于直线l对称,求实数m的值;
![]() 若直线与曲线相交于P,Q两点,且
若直线与曲线相交于P,Q两点,且![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为![]() ,参加第五项不合格的概率为
,参加第五项不合格的概率为![]()
(1)求该生被录取的概率;
(2)记该生参加考试的项数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com