
【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
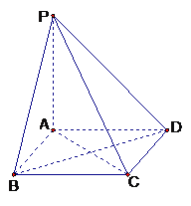
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
【答案】(1)证明见解析(2)![]()
【解析】
(1)建立空间直角坐标系,再利用向量的数量积运算,证明线线垂直,从而证明线面垂直;
(2)建立空间直角坐标系,求平面的法向量,再利用数量积求向量的夹角即可得解.
解:(1)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=![]() ,
,
∴AB=2.∴B(2,0,0)、C(2,2,0),
∴![]()
∵![]() ,即BD⊥AP,BD⊥AC,
,即BD⊥AP,BD⊥AC,
又AP∩AC=A,
故BD⊥平面PAC.
(2)由(1)得![]() .
.
设平面PCD的法向量为![]() ,则
,则![]() ,
,
即![]() ,∴
,∴![]() ,故平面PCD的法向量可取为
,故平面PCD的法向量可取为![]() ,
,
∵PA⊥平面ABCD,∴![]() 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P—CD—B的大小为,依题意可得 ,
,
故二面角P—CD—B余弦值的大小为![]() .
.



 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 上的点到右焦点F的最大距离为
上的点到右焦点F的最大距离为![]() ,离心率为
,离心率为![]() .
.
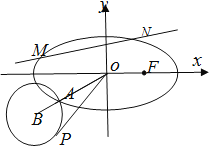
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 如图,过点
如图,过点![]() 的动直线l交椭圆C于M,N两点,直线l的斜率为
的动直线l交椭圆C于M,N两点,直线l的斜率为![]() ,A为椭圆上的一点,直线OA的斜率为
,A为椭圆上的一点,直线OA的斜率为![]() ,且
,且![]() ,B是线段OA延长线上一点,且
,B是线段OA延长线上一点,且![]() 过原点O作以B为圆心,以
过原点O作以B为圆心,以![]() 为半径的圆B的切线,切点为
为半径的圆B的切线,切点为![]() 令
令![]() ,求
,求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
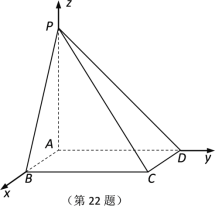
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,当点E在B1D1(与B1,D1不重合)上运动时,总有:
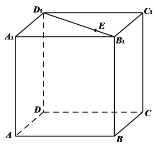
①AE∥BC1; ②平面AA1E⊥平面BB1D1D;
③AE∥平面BC1D; ④A1C⊥AE.
以上四个推断中正确的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4名运动员参加一次乒乓球比赛,每![]() 名运动员都赛
名运动员都赛![]() 场并决出胜负.设第
场并决出胜负.设第![]() 位运动员共胜
位运动员共胜![]() 场,负
场,负![]() 场
场![]() ,则错误的结论是( )
,则错误的结论是( )
A. ![]()
B. ![]()
C. ![]() 为定值,与各场比赛的结果无关
为定值,与各场比赛的结果无关
D. ![]() 为定值,与各场比赛结果无关
为定值,与各场比赛结果无关
查看答案和解析>>
科目:高中数学 来源: 题型:
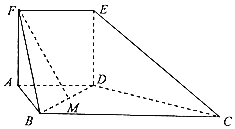
【题目】如图,在多面体![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com