
【题目】在平面直角坐标系xOy中,直线l: 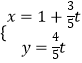 (t为参数),与曲线C:
(t为参数),与曲线C: ![]() (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
【答案】解:(方法一)直线l的参数方程化为普通方程得4x﹣3y=4, 将曲线C的参数方程化为普通方程得y2=4x.
联立方程组 ![]() 解得
解得 ![]() ,或
,或 
所以A(4,4),B( ![]() ,﹣1).
,﹣1).
所以AB═ ![]() .
.
(方法二)将曲线C的参数方程化为普通方程得y2=4x.
直线l的参数方程代入抛物线C的方程得 ( ![]() t)2=4(1+
t)2=4(1+ ![]() ),即4t2﹣15t﹣25=0,
),即4t2﹣15t﹣25=0,
所以 t1+t2= ![]() ,t1t2=﹣
,t1t2=﹣ ![]()
所以AB=|t1﹣t2|= ![]() =
= ![]()
【解析】方法一:直线l的参数方程化为普通方程得4x﹣3y=4,将曲线C的参数方程化为普通方程得y2=4x.联立求出交点坐标,利用两点之间的距离公式即可得出.方法二:将曲线C的参数方程化为普通方程得y2=4x. 直线l的参数方程代入抛物线C的方程得 4t2﹣15t﹣25=0,利用AB=|t1﹣t2|= ![]() 即可得出.
即可得出.


科目:高中数学 来源: 题型:
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
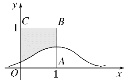
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司年初用81万元购买一艘捕鱼船,第一年各种费用为1万元,以后每年都增加2万元,每年捕鱼收益30万元.
![]() 问第几年开始获利?
问第几年开始获利?
![]() 若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
方案二:总纯收入获利最大时,以10万元出售该渔船![]() 问:哪一种方案合算?请说明理由.
问:哪一种方案合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,摩天轮的半径为![]() ,
,![]() 点距地面的高度为
点距地面的高度为![]() ,摩天轮按逆时针方向作匀速运动,且每
,摩天轮按逆时针方向作匀速运动,且每![]() 转一圈,摩天轮上点
转一圈,摩天轮上点![]() 的起始位置在最高点.
的起始位置在最高点.

(1)试确定点![]() 距离地面的高度
距离地面的高度![]() (单位:
(单位:![]() )关于旋转时间
)关于旋转时间![]() (单位:
(单位:![]() )的函数关系式;
)的函数关系式;
(2)在摩天轮转动一圈内,有多长时间![]() 点距离地面超过
点距离地面超过![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知![]() ,
,![]() ,且函数
,且函数![]() 的图像上的任意两条对称轴之间的距离的最小值是
的图像上的任意两条对称轴之间的距离的最小值是![]() .
.
(1)求![]() 的值:
的值:
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 单位后,得到函数
单位后,得到函数![]() 的图像,求函数
的图像,求函数![]() 在
在![]() 上的最值,并求取得最值时的
上的最值,并求取得最值时的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com