
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2. 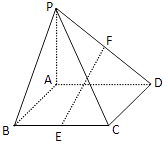
(1)求证:EF∥平面PAB.
(2)求直线EF与平面PCD所成的角.
【答案】
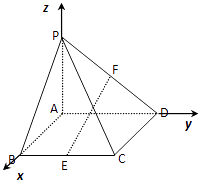
(1)证明:依题意,以A为原点,分别以AB、AD、AP所在
直线为x轴、y轴、z轴,建立空间直角坐标系如图,则A(0,0,0),B(2,0,0),P(0,0,4),D(0,4,0)C(2,4,0),E(2,2,0),F(0,2,2)
∴ ![]() =(﹣2,0,2),平面PAB的一个法向量是
=(﹣2,0,2),平面PAB的一个法向量是 ![]() =(0,4,0)
=(0,4,0)
∵ ![]() =0,
=0,
∴ ![]() ,
,
故 EF∥平面PAB
(2)∵ ![]() =(2,0,0),
=(2,0,0), ![]() =(0,﹣4,4).
=(0,﹣4,4).
设平面PCD的一个法向量为 ![]() =(x,y,z)
=(x,y,z)
则 ![]() 得
得 ![]() ∴令z=1,得
∴令z=1,得 ![]() =(0,1,1)
=(0,1,1)
而 ![]() =(﹣2,0,2),
=(﹣2,0,2),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∴< ![]() ,
, ![]() >=60°
>=60°
所以EF与平面PCD所成的角是90°﹣60°=30°
【解析】(1)以A为原点,分别以AB、AD、AP所在直线为x轴、y轴、z轴,建立空间直角坐标系, ![]() =(﹣2,0,2),平面PAB的一个法向量是
=(﹣2,0,2),平面PAB的一个法向量是 ![]() =(0,4,0),证明
=(0,4,0),证明 ![]() ,即可证明EF∥平面PAB;(2)求出平面PCD的一个法向量,即可求直线EF与平面PCD所成的角.
,即可证明EF∥平面PAB;(2)求出平面PCD的一个法向量,即可求直线EF与平面PCD所成的角.
【考点精析】利用直线与平面平行的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则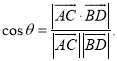 .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)的导函数为f′(x),满足f′(x)<f(x),且f(0)=1,则不等式f(x)<ex的解集为( )
A.(﹣∞,e4)
B.(e4 , +∞)
C.(﹣∞,0)
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的导函数为f′(x),对任意的x∈R都有3f′(x)>f(x)成立,则( )
A.3f(3ln2)>2f(3ln3)
B.3f(3ln2)与2f(3ln3)的大小不确定
C.3f(3ln2)=2f(3ln3)
D.3f(3ln2)<2f(3ln3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个说法: ①若向量{ ![]() 、
、 ![]() 、
、 ![]() }是空间的一个基底,则{
}是空间的一个基底,则{ ![]() +
+ ![]() 、
、 ![]() ﹣
﹣ ![]() 、
、 ![]() }也是空间的一个基底.
}也是空间的一个基底.
②空间的任意两个向量都是共面向量.
③若两条不同直线l,m的方向向量分别是 ![]() 、
、 ![]() ,则l∥m
,则l∥m ![]() ∥
∥ ![]() .
.
④若两个不同平面α,β的法向量分别是 ![]() 、
、 ![]() ,且
,且 ![]() =(1,2,﹣2)、
=(1,2,﹣2)、 ![]() =(﹣2,﹣4,4),则α∥β.
=(﹣2,﹣4,4),则α∥β.
其中正确的说法的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(πx+ ![]() )和函数g(x)=cos(πx+
)和函数g(x)=cos(πx+ ![]() )在区间[﹣
)在区间[﹣ ![]() ,
, ![]() ]上的图象交于A,B,C三点,则△ABC的面积是( )
]上的图象交于A,B,C三点,则△ABC的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在D上的函数f(x),若存在距离为d的两条直线y=kx+m1和y=kx+m2 , 使得对任意x∈D都有kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)(x∈D)有一个宽度为d的通道.给出下列函数: ①f(x)= ![]() ;
;
②f(x)=sinx;
③f(x)= ![]() ;
;
④f(x)= ![]()
其中在区间[1,+∞)上通道宽度可以为1的函数有(写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=f(x)的图象向右平移 ![]() 单位得到函数y=cos2x的图象,则f(x)=( )
单位得到函数y=cos2x的图象,则f(x)=( )
A.﹣sin2x
B.cos2x
C.sin2x
D.﹣cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s ![]() 和s
和s ![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率. 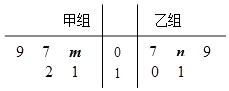
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com