
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
【答案】(1)![]() ;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
【解析】
(1)先求解等差数列![]() 的通项公式,再根据
的通项公式,再根据![]() 求解
求解![]() 的通项公式;(2)①采用错位相减法先求
的通项公式;(2)①采用错位相减法先求![]() ,再根据
,再根据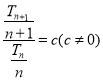 ,证明
,证明![]() 为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即
为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即![]() 取什么值时能满足要求.
取什么值时能满足要求.
(1)因为![]() ,所以
,所以![]()
所以![]()
即![]()
当![]() 时,
时,![]()
∴![]()
当n=1时,![]() ,符合上述通项,所以
,符合上述通项,所以![]()
(2)①因为![]() ,所以
,所以![]()
所以![]()
则![]()
两式相减,可整理得![]()
∴![]() ,
,![]() ,且
,且![]()
所以数列![]() 是以4为首项,2为公比的等比数列.
是以4为首项,2为公比的等比数列.
②由①可知,![]() ,且由(1)知
,且由(1)知![]() ,代入
,代入![]()
可得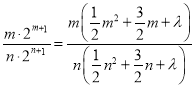
整理得![]()
即:![]() ,设
,设![]() ,则
,则![]()
则![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,且
,且![]()
所以![]()
所以![]() 或
或![]() ,即n=2,m=4或3
,即n=2,m=4或3
当n=2,m=4时,λ=-2,
当n=2,m=3时,λ=-1.


科目:高中数学 来源: 题型:
【题目】某研究性学习小组对无现金支付(支付宝、微信、银行卡)的用户进行问卷调查,随机选取了![]() 人(图1),按年龄分为青年组与中老年组,如图2.
人(图1),按年龄分为青年组与中老年组,如图2.
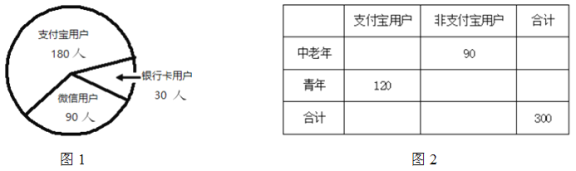
(1)完成图2的列联表,并判断是否有![]() 的把握认为使用支付宝用户与年龄有关系?
的把握认为使用支付宝用户与年龄有关系?
(2)现从调查的中老年组中按分层抽样的方法选出![]() 人,再随机抽取
人,再随机抽取![]() 人赠送礼品,试求抽取的
人赠送礼品,试求抽取的![]() 人中恰有
人中恰有![]() 人为“非支付宝用户”的概率.
人为“非支付宝用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+![]() ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,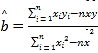 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的奇函数![]() 满足
满足![]() ,且
,且![]() 时,
时, ![]() ,下面四种说法①
,下面四种说法①![]() ;②函数
;②函数![]() 在[-6,-2]上是增函数;③函数
在[-6,-2]上是增函数;③函数![]() 关于直线
关于直线![]() 对称;④若
对称;④若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在[-8,8]上所有根之和为-8,其中正确的序号__________。
在[-8,8]上所有根之和为-8,其中正确的序号__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.
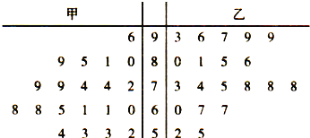
(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率.
(2)由以上统计数据填写下面2×2列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
![]()
附:临界值表
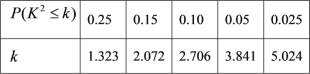
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,整理如下:
甲公司员工![]() :410,390,330,360,320,400,330,340,370,350
:410,390,330,360,320,400,330,340,370,350
乙公司员工![]() :360,420,370,360,420,340,440,370,360,420
:360,420,370,360,420,340,440,370,360,420
每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件0.65元,乙公司规定每天350件以内(含350件)的部分每件0.6元,超出350件的部分每件0.9元.
(1)根据题中数据写出甲公司员工![]() 在这10天投递的快件个数的平均数和众数;
在这10天投递的快件个数的平均数和众数;
(2)为了解乙公司员工![]() 每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据题中数据估算两公司被抽取员工在该月所得的劳务费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校共有学生2000人,其中男生900人,女生1100人,为了调查该校学生每周平均体育锻炼时间,采用分层抽样的方法收集该校100名学生每周平均体育锻炼时间(单位:小时).
(1)应抽查男生与女生各多少人?
(2)根据收集100人的样本数据,得到学生每周平均体育锻炼时间的频率分布表:
时间(小时) | [0,1] | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] |
频率 | 0.05 | 0.20 | 0.30 | 0.25 | 0.15 | 0.05 |
若在样本数据中有38名男学生平均每周课外体育锻炼时间超过2小时,请完成每周平均体育锻炼时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关”?
男生 | 女生 | 总计 | |
每周平均体育锻炼时间不超过2小时 | |||
每周平均体育锻炼时间超过2小时 | |||
总计 |
附:K2![]() .
.
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com