练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列四个命题：

    ①函数的最大值为1；

    ②已知集合，则集合A的真子集个数为3；

    ③若为锐角三角形，则有；

    ④“”是“函数在区间内单调递增”的充分必要条件.

    其中正确的命题是______.（填序号）

    【答案】②③④

    【解析】

    由二倍角公式结合正弦函数的性质判断①；由集合的知识判断②；由锐角三角形的定义以及正弦函数的单调性，结合诱导公式判断③；由二次函数的图象和性质，集合充分必要条件的定义判断④.

    由，得的最大值为，故①错误；

    ，则集合的真子集为，共有三个，故②正确；

    为锐角三角形，，则

    在上为增函数，

    同理可证，

    ，故③正确；

    当时，函数在区间的解析式为，由对称轴可知，函数在区间内单调递增

    若函数在区间内单调递增，结合二次函数的对称轴，可知，则

    即“”是“函数在区间内单调递增”的充分必要条件.故④正确；

    故答案为：②③④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，已知动直线的参数方程：，（为参数，） ，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）求曲线的直角坐标方程；

    （Ⅱ）若直线与曲线恰好有2个公共点时，求直线的一般方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）当时，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.

    （1）证明：平面AEC；

    （2）设AP＝1，AD＝，三棱锥P－ABD的体积V＝，求A到平面PBC的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，底面为菱形， ， ， 与相交于点，四边形为直角梯形， ， ， ，平面底面.

    （1）证明：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求曲线在点处切线的方程；

    （Ⅱ）求函数的单调区间；

    （Ⅲ）当时，恒成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，、是过点夹角为的两条直线，且与圆心为，半径长为的圆分别相切，设圆周上一点到、的距离分别为、，那么的最小值为（____）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将编号为1，2，…，18的18名乒乓球运动员分配在9张球台上进行单打比赛，规定每一张球台上两选手编号之和均为大于4的平方数．记{7号与18号比赛}为事件p．则p为（　　）．

    A. 不可能事件 B. 概率为的随机事件

    C. 概率为的随机事件 D. 必然事件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，平面平面，为棱上的一点，且，为棱的中点，为棱上的一点，若平面，是边长为4的正三角形，，.

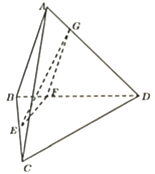
    （1）求证：平面平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案