
【题目】已知函数![]() ,且
,且![]() 在
在![]() 上满足
上满足![]() 恒成立.
恒成立.
(1)求实数![]() 的值;
的值;
(2)令![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)分别在![]() 和
和![]() 两种情况下讨论导函数的正负,得到原函数单调性,由此可知
两种情况下讨论导函数的正负,得到原函数单调性,由此可知![]() 时不合题意,并求出
时不合题意,并求出![]() 时,
时,![]() ,则只需
,则只需![]() 即可,令
即可,令![]() ,利用导数可求得
,利用导数可求得![]() ,结合
,结合![]() ,由此可确定仅有
,由此可确定仅有![]() 满足条件;
满足条件;
(2)利用导数和零点存在性定理可确定函数![]() 的单调性,得到
的单调性,得到![]() ,由
,由![]() 可化简得到
可化简得到![]() ,代入
,代入![]() 解析式即可证得结论.
解析式即可证得结论.
(1)当![]() 时,原函数可化为:
时,原函数可化为:![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() 当
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,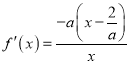 ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,
上单调递减,
即![]() .
.
![]() 要使
要使![]() 在
在![]() 时恒成立,则只需
时恒成立,则只需![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() 满足条件的
满足条件的![]() 只有
只有![]() ,即
,即![]() .
.
(2)由(1)知:![]() ,
,![]() ,
,
![]() ,
,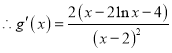 .
.
令![]() ,则
,则![]() ,
,
![]() ,
,![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
又![]() ,
,![]() ,
,
![]() ,使得
,使得![]() ,即
,即![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() ,
,
![]() ,
,
即![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】方程x2+![]() x-1=0的解可视为函数y=x+
x-1=0的解可视为函数y=x+![]() 的图象与函数y=
的图象与函数y=![]() 的图象交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi ,
的图象交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi ,![]() )(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点E是棱BC的中点,
,点E是棱BC的中点,![]() ,点P在平面ABCD的射影为O,F为棱PA上一点.
,点P在平面ABCD的射影为O,F为棱PA上一点.
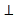
![]() 1
1![]() 求证:平面
求证:平面![]() 平面BCF;
平面BCF;
![]() 2
2![]() 若
若![]() 平面PDE,
平面PDE,![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: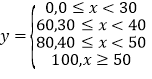 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
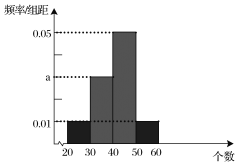
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的函数f(x)是最小正周期为2π的偶函数,f'(x)是f(x)的导函数,当x∈[0,π]时,0≤f(x)≤1;当x∈(0,π)且x≠![]() 时,
时,![]() ,则函数y=f(x)-|sinx|在区间
,则函数y=f(x)-|sinx|在区间![]() 上的零点个数为( )
上的零点个数为( )
A. 4 B. 6 C. 7 D. 8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的焦点为F,点P是半椭圆
的焦点为F,点P是半椭圆![]() 上的一点,过点P作抛物线C的两条切线,切点分别为A、B,且直线PA、PB分别交y轴于点M、N.
上的一点,过点P作抛物线C的两条切线,切点分别为A、B,且直线PA、PB分别交y轴于点M、N.
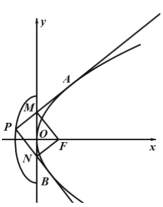
(1)证明:![]() ;
;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() .
.
(1)若a是从0、1、2、3四个数中任取的一个数,是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率.
(2)若a是从区间![]() 内任取的一个数,
内任取的一个数,![]() ,求上述方程没有实根的概率.
,求上述方程没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com