
”¾ĢāÄæ”æ2020Äźŗ®¼ŁĘŚ¼ä£¬Ä³øßÖŠ¾ö¶ØÉīČėµ÷²é±¾Š£Ń§Éśŗ®¼ŁĘŚ¼äŌŚ¼ŅѧĻ°Ēéæö£¬²¢½«ŅĄ¾Żµ÷²é½į¹ū¶ŌĻąÓ¦Ń§ÉśĢį³öÕė¶ŌŠŌѧĻ°½ØŅ飮ĻÖ“Ó±¾Š£øßŅ»”¢ø߶ž”¢øßȿȿøöÄź¼¶ÖŠ·Ö±šĖ껜єȔ30£¬45£¬75ČĖ£¬Č»ŗóŌŁ“ÓÕāŠ©Ń§ÉśÖŠ³éČ”10ČĖ£¬½ųŠŠŃ§Ēéµ÷²é£®
£Ø1£©Čō²ÉÓĆ·Ö²ć³éŃł³éČ”10ČĖ£¬·Ö±šĒóøßŅ»”¢ø߶ž”¢øßČżÓ¦³éČ”µÄČĖŹż£®
£Ø2£©Čō±»³éČ”µÄ10ČĖÖŠ£¬ÓŠ6ČĖĆæĢģѧŹ±³¬¹ż7Š”Ź±£¬ÓŠ4ČĖĆæĢģѧŹ±²»×ć4Š”Ź±£¬ĻÖ“ÓÕā10ČĖÖŠ£¬ŌŁĖ껜³éČ”4ČĖ×ö½ųŅ»²½µ÷²é£®
£Øi£©¼ĒŹĀ¼žAĪŖ”°±»³éČ”µÄ4ČĖÖŠÖĮ¶ąÓŠ1ČĖѧŹ±²»×ć4Š”Ź±”±£¬ĒóŹĀ¼žA·¢ÉśµÄøÅĀŹ£»
£Øii£©ÓƦĪ±ķŹ¾±»³éČ”µÄ4ČĖ֊ѧŹ±²»×ć4Š”Ź±µÄČĖŹż£¬ĒóĖ껜±äĮæ¦ĪµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£®
”¾“š°ø”æ£Ø1£©øßŅ»”¢ø߶ž”¢øßČżÓ¦³éČ”µÄČĖŹż·Ö±šĪŖ2ČĖ£¬3ČĖ£¬5ČĖ£»£Ø2£©£Øi£©![]() £»£Øii£©¼ū½āĪö£¬
£»£Øii£©¼ū½āĪö£¬![]()
”¾½āĪö”æ
£Ø1£©×ÜŹżĪŖ30+45+75=150£¬“ÓÕāŠ©Ń§ÉśÖŠ³éČ”10ČĖ£¬øł¾Ż·Ö²ć³éŃł·ØĒó³öøßŅ»”¢ø߶ž”¢øßČżÓ¦³éČ”µÄČĖŹż¼“æÉ£»
£Ø2£©£Øi£©¼ĒŹĀ¼žAĪŖ”°±»³éČ”µÄ4ČĖÖŠÖĮ¶ąÓŠ1ČĖѧŹ±²»×ć4Š”Ź±”±£¬¼ĒŹĀ¼žBĪŖ”°±»³éČ”µÄ4ČĖÖŠĒ”ÓŠ1ČĖѧŹ±²»×ć4Š”Ź±”±£¬¼ĒŹĀ¼žCĪŖ”°±»³éČ”µÄ4ČĖÖŠĒ”ÓŠ0ČĖѧŹ±²»×ć4Š”Ź±”±£¬ŌņÓÉP(A)£½P(B”ČC)£½P(B)+P(C)£¬Ēó³öøÅĀŹ¼“æÉ£»
£Øii£©Ė껜±äĮæ¦Ī±ķŹ¾±»³éČ”µÄ4ČĖ֊ѧŹ±²»×ć4Š”Ź±µÄČĖŹż£¬Ōņ¦Ī£½0£¬1£¬2£¬3£¬4£¬Ēó³öĖ껜±äĮæ¦ĪµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū¼“æÉ£®
£Ø1£©“Ó±¾Š£øßŅ»”¢ø߶ž”¢øßȿȿøöÄź¼¶ÖŠ·Ö±šĖ껜єȔ30£¬45£¬75ČĖ£¬
30+45+75=150£¬
“ÓÕāŠ©Ń§ÉśÖŠ³éČ”10ČĖ£¬øł¾Ż·Ö²ć³éŃł·Ø£¬øßŅ»Ó¦³éČ”10![]() 2ČĖ£¬ø߶žÓ¦³éČ”10
2ČĖ£¬ø߶žÓ¦³éČ”10![]() ČĖ£¬øßČżÓ¦³éČ”10
ČĖ£¬øßČżÓ¦³éČ”10![]() ČĖ£¬
ČĖ£¬
¹ŹøßŅ»”¢ø߶ž”¢øßČżÓ¦³éČ”µÄČĖŹż·Ö±šĪŖ2ČĖ£¬3ČĖ£¬5ČĖ£»
£Ø2£©£Øi£©¼ĒŹĀ¼žAĪŖ”°±»³éČ”µÄ4ČĖÖŠÖĮ¶ąÓŠ1ČĖѧŹ±²»×ć4Š”Ź±”±£¬¼ĒŹĀ¼žBĪŖ”°±»³éČ”µÄ4ČĖÖŠĒ”ÓŠ1ČĖѧŹ±²»×ć4Š”Ź±”±£¬¼ĒŹĀ¼žCĪŖ”°±»³éČ”µÄ4ČĖÖŠĒ”ÓŠ0ČĖѧŹ±²»×ć4Š”Ź±”±£¬ŌņP(A)£½P(B”ČC)£½P(B)+P(C)![]() £»
£»
£Øii£©Ė껜±äĮæ¦Ī±ķŹ¾±»³éČ”µÄ4ČĖ֊ѧŹ±²»×ć4Š”Ź±µÄČĖŹż£¬Ōņ¦Ī£½0£¬1£¬2£¬3£¬4£¬
Ōņ![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
Ė껜±äĮæ¦ĪµÄ·Ö²¼ĮŠČēĻĀ£ŗ
¦Ī | 0 | 1 | 2 | 3 | 4 |
P |
|
|
| |
|
E(¦Ī)![]() £®
£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖČżĄāÖłABC-A1B1C1µÄµ×ĆęŹĒÕżČż½ĒŠĪ£¬²ąĆęBB1C1CŹĒ¾ŲŠĪ£¬M£¬N·Ö±šĪŖBC£¬B1C1µÄÖŠµć£¬PĪŖAMÉĻŅ»µć£¬¹żB1C1ŗĶPµÄĘ½Ćę½»ABÓŚE£¬½»ACÓŚF.
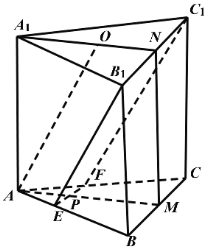
£Ø1£©Ö¤Ć÷£ŗAA1”ĪMN£¬ĒŅĘ½ĆęA1AMN”ĶEB1C1F£»
£Ø2£©ÉčOĪŖ”÷A1B1C1µÄÖŠŠÄ£¬ČōAO”ĪĘ½ĆęEB1C1F£¬ĒŅAO=AB£¬ĒóÖ±ĻßB1EÓėĘ½ĆęA1AMNĖł³É½ĒµÄÕżĻŅÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() ŹĒ¶ØŅåŌŚRÉĻµÄĘęŗÆŹż£¬µ±
ŹĒ¶ØŅåŌŚRÉĻµÄĘęŗÆŹż£¬µ±![]() Ź±£¬
Ź±£¬![]() £¬øų³öĻĀĮŠĆüĢā£ŗ
£¬øų³öĻĀĮŠĆüĢā£ŗ
¢Łµ±![]() Ź±£¬
Ź±£¬![]() £»
£»
¢ŚŗÆŹż![]() ÓŠ2øöĮćµć£»
ÓŠ2øöĮćµć£»
¢Ū![]() µÄ½ā¼ÆĪŖ
µÄ½ā¼ÆĪŖ![]() £»
£»
¢Ü![]() £¬
£¬![]() £¬¶¼ÓŠ
£¬¶¼ÓŠ![]() .
.
ĘäÖŠÕęĆüĢāµÄøöŹżĪŖ£Ø £©
A.4B.3C.2D.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹ®ĪåĒɰ唢ÓÖ³ĘŅęÖĒĶ¼£¬ĪŖĒå³ÆÕć½Ź”µĀĒåÖŖĻŲĶÆŅ¶øżŌŚĶ¬ÖĪÄź¼äĖł·¢Ć÷£¬ĖüÄÜĘ“³ö²ŻÄ¾”¢»Ø¹ū”¢ÄńŹŽ”¢Óć³ę”¢ĪÄ×ÖµČĶ¼°ø.Ź®ĪåĒÉ°åÓÉŹ®Īåæé°å×é³ÉŅ»øö“óÕż·½ŠĪ£ØČēĶ¼1£©£¬ĘäÖŠ±źŗÅĪŖ2£¬3£¬4£¬5µÄŠ”°å¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Ķ¼2ŹĒÓĆŹ®ĪåĒÉ°åĘ“³öµÄ2019ğɜŠ¤ÖķµÄĶ¼°ø£¬Ōņ“ÓÉśŠ¤ÖķĶ¼°øÖŠČĪČ”Ņ»µć£¬øƵćĒ”ŗĆČ”×ŌŅõÓ°²æ·ÖÖŠµÄøÅĀŹĪŖ______.
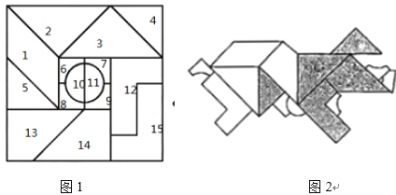
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĮ½øöÕż·½ŠĪABCDŗĶCDEFÓŠŅ»Ģõ¹«¹²±ßCD£¬ĒŅ”÷BCFŹĒµČ±ßČż½ĒŠĪ£¬ŌņŅģĆęÖ±ĻßACŗĶDFĖł³É½ĒµÄÓąĻŅÖµĪŖ£Ø £©
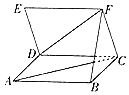
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©£½2|x+2|+|x©3|£®
£Ø1£©Ēó²»µČŹ½f£Øx£©”Ż8µÄ½ā¼Æ£»
£Ø2£©Čōa£¾0£¬b£¾0£¬ĒŅŗÆŹżF£Øx£©£½f£Øx£©©3a©2bÓŠĪØŅ»Įćµćx0£¬Ö¤Ć÷£ŗ![]() f£Øx0£©£®
f£Øx0£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĶÖŌ²![]() ¹żµć
¹żµć![]() £¬ĄėŠÄĀŹĪŖ
£¬ĄėŠÄĀŹĪŖ![]() £¬
£¬![]() ·Ö±šŹĒĶÖŌ²
·Ö±šŹĒĶÖŌ²![]() µÄ×ó”¢ÓŅ¶„µć£¬¹żÓŅ½¹µć
µÄ×ó”¢ÓŅ¶„µć£¬¹żÓŅ½¹µć![]() ĒŅŠ±ĀŹĪŖ
ĒŅŠ±ĀŹĪŖ![]() µÄÖ±Ļß
µÄÖ±Ļß![]() ÓėĶÖŌ²
ÓėĶÖŌ²![]() Ļą½»ÓŚ
Ļą½»ÓŚ![]() Į½µć£®
Į½µć£®
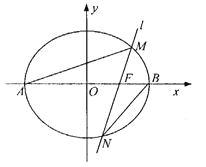
£Ø1£©ĒóĶÖŌ²![]() µÄ±ź×¼·½³Ģ£»
µÄ±ź×¼·½³Ģ£»
£Ø2£©¼Ē![]() ”¢
”¢![]() µÄĆ껿·Ö±šĪŖ
µÄĆ껿·Ö±šĪŖ![]() ”¢
”¢![]() £¬Čō
£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©¼ĒÖ±Ļß![]() ”¢
”¢![]() µÄŠ±ĀŹ·Ö±šĪŖ
µÄŠ±ĀŹ·Ö±šĪŖ![]() ”¢
”¢![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2019Äźµ×£¬ŗž±±Ź”ĪäŗŗŹŠµČ¶ąøöµŲĒųĀ½Šų³öĻÖøŠČ¾ŠĀŠĶ¹Ś×“²”¶¾·ĪŃ׵Ļ¼Õß.ĪŖ¼°Ź±ÓŠŠ§µŲ¶ŌŅßĒ鏿¾Ż½ųŠŠĮ÷ŠŠ²”ѧĶ³¼Ę·ÖĪö£¬Ä³µŲŃŠ¾æ»ś¹¹Õė¶ŌøƵŲŹµ¼ŹĒéæö£¬øł¾ŻøƵŲ»¼ÕߏĒ·ńÓŠĪäŗŗĀĆŠŠŹ·ÓėŹĒ·ńÓŠČ·Õļ²”Ąż½Ó“„Ź·£¬½«ŠĀ¹Ś·ĪŃ×»¼Õß·ÖĪŖĖÄĄą£ŗÓŠĪäŗŗĀĆŠŠŹ·£ØĪŽ½Ó“„Ź·£©£¬ĪŽĪäŗŗĀĆŠŠŹ·£ØĪŽ½Ó“„Ź·£©£¬ÓŠĪäŗŗĀĆŠŠŹ·£ØÓŠ½Ó“„Ź·£©ŗĶĪŽĪäŗŗĀĆŠŠŹ·£ØÓŠ½Ó“„Ź·£©£¬Ķ³¼ĘµĆµ½ŅŌĻĀĻą¹ŲŹż¾Ż.
£Ø1£©Ēė½«ĮŠĮŖ±ķĢīŠ“ĶźÕū£ŗ
ÓŠ½Ó“„Ź· | ĪŽ½Ó“„Ź· | ×Ü¼Ę | |
ÓŠĪäŗŗĀĆŠŠŹ· | 27 | ||
ĪŽĪäŗŗĀĆŠŠŹ· | 18 | ||
×Ü¼Ę | 27 | 54 |
£Ø2£©ÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.025µÄĒ°ĢįĻĀČĻĪŖÓŠĪäŗŗĀĆŠŠŹ·ÓėÓŠČ·Õļ²”Ąż½Ó“„Ź·ÓŠ¹ŲĻµ£æ
ø½£ŗ![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() µÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øų³öĖÄøöŗÆŹż£ŗ¢Ł
µÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øų³öĖÄøöŗÆŹż£ŗ¢Ł![]() £¬¢Ś
£¬¢Ś![]() £¬¢Ū
£¬¢Ū![]() £¬¢Ü
£¬¢Ü![]() £¬ÓÖøų³öĖÄøöŗÆŹżµÄĶ¼Ļó£¬ŌņÕżČ·µÄĘ„Åä·½°øŹĒ£Ø £©£®
£¬ÓÖøų³öĖÄøöŗÆŹżµÄĶ¼Ļó£¬ŌņÕżČ·µÄĘ„Åä·½°øŹĒ£Ø £©£®
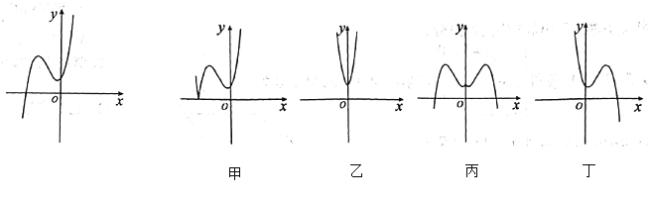
A.¢Ł£¼×£¬¢Ś£ŅŅ£¬¢Ū£±ū£¬¢Ü£¶”B.¢Ś£¼×£¬¢Ł£ŅŅ£¬¢Ū£±ū£¬¢Ü£±ū
C.¢Ł£¼×£¬¢Ū£ŅŅ£¬¢Ü£±ū£¬¢Ś£¶”D.¢Ł£¼×£¬¢Ü£ŅŅ£¬¢Ū£±ū£¬¢Ś£¶”
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com