练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的图象如图所示，给出四个函数：①，②，③，④，又给出四个函数的图象，则正确的匹配方案是（ ）．

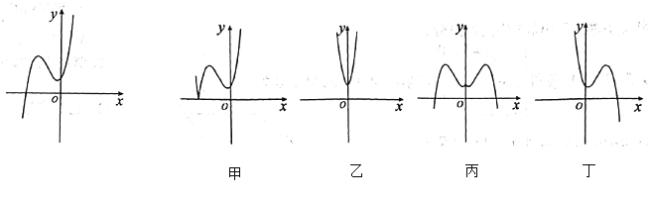
    A.①－甲，②－乙，③－丙，④－丁B.②－甲，①－乙，③－丙，④－丙

    C.①－甲，③－乙，④－丙，②－丁D.①－甲，④－乙，③－丙，②－丁

    【答案】A

    【解析】

    结合函数图象的变换进行求解，①可以翻折图象得到，②③④可以通过对称得到.

    把的图象轴下方的部分翻折到上方，上方部分保持不变可得的图象，所以①-甲；

    把的图象轴左边的部分去掉，轴右边的部分保持不变，同时把轴右边的图象对称到轴左边，可得的图象，所以②-乙；

    把的图象轴右边的部分去掉，轴左边的部分保持不变，同时把轴左边的图象对称到轴右边，可得的图象，所以③-丙；

    作的图象关于轴的对称图象，可得的图象，所以④-丁；

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2020年寒假期间，某高中决定深入调查本校学生寒假期间在家学习情况，并将依据调查结果对相应学生提出针对性学习建议．现从本校高一、高二、高三三个年级中分别随机选取30，45，75人，然后再从这些学生中抽取10人，进行学情调查．

    （1）若采用分层抽样抽取10人，分别求高一、高二、高三应抽取的人数．

    （2）若被抽取的10人中，有6人每天学时超过7小时，有4人每天学时不足4小时，现从这10人中，再随机抽取4人做进一步调查．

    （i）记事件A为“被抽取的4人中至多有1人学时不足4小时”，求事件A发生的概率；

    （ii）用ξ表示被抽取的4人中学时不足4小时的人数，求随机变量ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为为参数，圆C的标准方程为以坐标原点为极点，x轴正半轴为极轴建立极坐标系．

    求直线l和圆C的极坐标方程；

    若射线与l的交点为M，与圆C的交点为A，B，且点M恰好为线段AB的中点，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，记为的导函数.

    （1）当时，若存在正实数，（）使得，证明：；

    （2）若存在大于1的实数，使得当时都有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一台仪器每启动一次都随机地出现一个位的二进制数，其中的各位数字中，出现的概率为，出现的概率为．若启动一次出现的数字为，则称这次试验成功．若成功一次得分，失败一次得分，则次这样的重复试验的总得分的数学期望和方差分别为（ ）

    A.，B.，C.，D.，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某正三棱锥的底面边长为4，侧面与底面所成二面角的余弦值为，球为该三棱锥的内切球.球与球相切，且与该三棱锥的三个侧面也相切，则球与球的表面积之比为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形为平行四边形，且，点E，F为平面外两点，且，．

    （1）证明：；

    （2）若，求异面直线与所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从甲、乙两种树苗中各抽测了10株树苗的高度，其茎叶图数据如图.根据茎叶图，下列描述正确的是（ ）

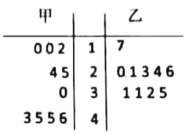
    A.甲种树苗的中位数大于乙种树苗的中位数，且甲种树苗比乙种树苗长得整齐

    B.甲种树苗的中位数大于乙种树苗的中位数，但乙种树苗比甲种树苗长得整齐

    C.乙种树苗的中位数大于甲种树苗的中位数，且乙种树苗比甲种树苗长得整齐

    D.乙种树苗的中位数大于甲种树苗的中位数，但甲种树苗比乙种树苗长得整齐

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知多面体是正方体，，分别是棱，的中点，点是棱上的动点，过点，，的平面与棱交于点，则以下说法不正确的是( )

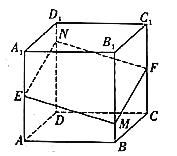
    A.四边形是平行四边形

    B.四边形是菱形

    C.当点从点往点运动时，四边形的面积先增大后减小

    D.当点从点往点运动时，三棱锥的体积一直增大

    查看答案和解析>>

    同步练习册答案