
【题目】已知数列![]() 的各项均为正数,且
的各项均为正数,且![]() ,对于任意的
,对于任意的![]() ,均有
,均有![]() ,
,![]() .
.
(1)求证:![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若数列![]() 中去掉
中去掉![]() 的项后,余下的项组成数列
的项后,余下的项组成数列![]() ,求
,求![]() ;
;
(3)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]()
![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() ,
,![]() ,且方程
,且方程![]()
![]() 有两个不相等的实根
有两个不相等的实根![]() 、
、![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,
,![]() ,
,![]() ,且a、b、c是三角形的三边长,试求满足等式:
,且a、b、c是三角形的三边长,试求满足等式:![]() 有解的最大的x的范围.
有解的最大的x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦曼德尔布罗在20世纪70年代创立的一门新的数学学科.它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图1所示的分形规律可得如图2所示的一个树形图:
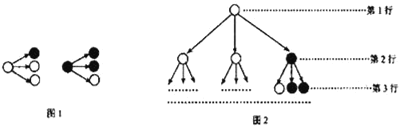
易知第三行有白圈5个,黑圈4个.我们采用“坐标”来表示各行中的白圈、黑圈的个数.比如第一行记为![]() ,第二行记为
,第二行记为![]() ,第三行记为
,第三行记为![]() .照此规律,第
.照此规律,第![]() 行中的白圈、黑圈的“坐标”为
行中的白圈、黑圈的“坐标”为![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() 的棱长为2,E、F、G分别为
的棱长为2,E、F、G分别为![]() 的中点,给出下列命题:
的中点,给出下列命题:
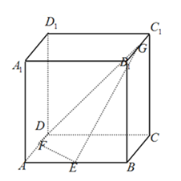
①异面直线EF与AG所成的角的余弦值为![]() ;
;
②过点E、F、G作正方体的截面,所得的截面的面积是![]() ;
;
③![]() 平面
平面![]()
④三棱锥![]() 的体积为1
的体积为1
其中正确的命题是_____________(填写所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装加工厂为了提高市场竞争力,对其中一台生产设备提出了甲、乙两个改进方案:甲方案是引进一台新的生产设备,需一次性投资1000万元,年生产能力为30万件;乙方案是将原来的设备进行升级改造,需一次性投入700万元,年生产能力为20万件.根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产设备还是改造原有的生产设备,设备的使用年限均为6年,该产品的销售利润为15元/件(不含一次性设备改进投资费用).
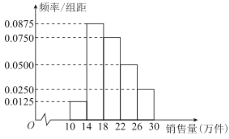
(1)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
①根据频率分布直方图估计年销售利润不低于270万元的概率:
②若以该生产设备6年的净利润的期望值作为决策的依据,试判断该服装厂应选择哪个方案.(6年的净利润=6年销售利润-设备改进投资费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子工厂生产一种电子元件,产品出厂前要检出所有次品.已知这种电子元件次品率为0.01,且这种电子元件是否为次品相互独立.现要检测3000个这种电子元件,检测的流程是:先将这3000个电子元件分成个数相等的若干组,设每组有![]() 个电子元件,将每组的
个电子元件,将每组的![]() 个电子元件串联起来,成组进行检测,若检测通过,则本组全部电子元件为正品,不需要再检测;若检测不通过,则本组至少有一个电子元件是次品,再对本组个电子元件逐一检测.
个电子元件串联起来,成组进行检测,若检测通过,则本组全部电子元件为正品,不需要再检测;若检测不通过,则本组至少有一个电子元件是次品,再对本组个电子元件逐一检测.
(1)当![]() 时,估算一组待检测电子元件中有次品的概率;
时,估算一组待检测电子元件中有次品的概率;
(2)设一组电子元件的检测次数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(3)估算当![]() 为何值时,每个电子元件的检测次数最小,并估算此时检测的总次数(提示:利用
为何值时,每个电子元件的检测次数最小,并估算此时检测的总次数(提示:利用![]() 进行估算).
进行估算).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com