
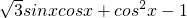 .
.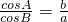 ,h(A)=
,h(A)= ,c=2,试求△ABC的面积.
,c=2,试求△ABC的面积.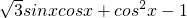 =
= sin2x-
sin2x- =sin2xcos
=sin2xcos +cos2xsin
+cos2xsin -
- ,
, )-
)- ,f(x)的最小正周期为T=
,f(x)的最小正周期为T= =π.
=π. =
= +kπ,得x=
+kπ,得x= +
+ kπ,k∈Z,所以函数图象的对称轴方程为:x=
kπ,k∈Z,所以函数图象的对称轴方程为:x= +
+ kπ,(k∈Z)
kπ,(k∈Z) +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,解之得-
+2kπ,解之得- +kπ≤x≤
+kπ≤x≤ +kπ,所以函数的单调增区间为[-
+kπ,所以函数的单调增区间为[- ,
, +kπ],(k∈Z)
+kπ],(k∈Z) +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z) x)=sin(
x)=sin( x+
x+ )-
)- ,
, x+
x+ )-
)- ;
; A+
A+ )-
)- =
= ,
, A+
A+ )=
)= ,结合A∈(0,π)得A=
,结合A∈(0,π)得A=
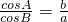 =
=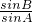

 ,所以△ABC是边长为2的等边三角形,
,所以△ABC是边长为2的等边三角形, ×22=
×22= .
. 时,因为c=2,A=
时,因为c=2,A= ,所以△ABC是斜边为2的直角三角形
,所以△ABC是斜边为2的直角三角形 =
= ,b=ccosA=2×
,b=ccosA=2× =1
=1 ×
× ×1=
×1= .
. 或
或 .
. )-
)- ,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间;
,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间; x+
x+ )-
)- ;
; ,再由
,再由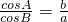 结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.
结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.

 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com