
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 都属于区间
都属于区间![]() 且
且![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(Ⅱ)
上单调递减;(Ⅱ)![]() .
.
【解析】
试题第一问对函数求导,结合参数的范围,确定出导数的符号,从而求得函数的单调性,第二问有两个自变量对应的函数值相等,从函数的单调区间出发,来研究对应的单调性,从而确定出参数所满足的不等关系,最后求得结果.
试题解析:(Ⅰ)![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上单调递增;
上单调递增;
![]() 当
当![]() 时,由
时,由![]() 得
得![]() ; 由
; 由![]() 得
得![]() ;
;
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知,当![]() 时,
时,![]() 在
在![]() 上单增,不合题意,故
上单增,不合题意,故![]() .
.
由![]() 则
则![]() ,即
,即![]()
即![]()
![]()
![]()
设![]()
![]()
![]() 在
在![]() 上恒成立;所以
上恒成立;所以![]() 在
在![]() 上递增,
上递增,
由![]() 式,函数
式,函数![]() 在
在![]() 有零点,则
有零点,则
![]()
故实数![]() 的取值范围为
的取值范围为![]() .12分
.12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有10位外国人,其中关注此次大阅兵的有8位,若从这10位外国人中任意选取3位做一次采访,则被采访者中至少有2位关注此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为正项等比数列,
为正项等比数列,![]() 为
为![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)从三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任选一个作为已知条件,求数列
中任选一个作为已知条件,求数列![]() 的前
的前![]() 项和
项和![]() .
.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全民抗击新冠肺炎疫情期间,北京市开展了“停课不停学”活动,此活动为学生提供了多种网络课程资源以供选择使用.活动开展一个月后,某学校随机抽取了高三年级的甲、乙两个班级进行网络问卷调查,统计学生每天的学习时间,将样本数据分成![]() 五组,并整理得到如下频率分布直方图:
五组,并整理得到如下频率分布直方图:
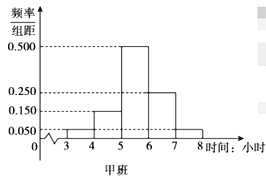
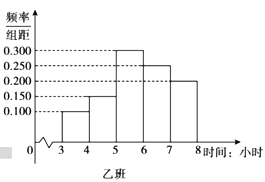
(1)已知该校高三年级共有600名学生,根据甲班的统计数据,估计该校高三年级每天学习时间达到5小时及以上的学生人数;
(2)已知这两个班级各有40名学生,从甲、乙两个班级每天学习时间不足4小时的学生中随机抽取3人,记从甲班抽到的学生人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记甲、乙两个班级学生每天学习时间的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
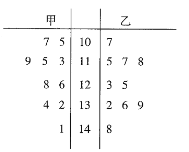
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)如果日销售额超过平均销售额,相应的电商即被评为优,根据统计数据估计两家电商一个月(按30天计算)被评为优的天数各是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
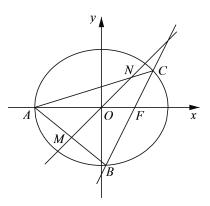
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com