
【题目】已知圆 ![]() :
: ![]() ,直线
,直线 ![]() :
: ![]() .
.
(1)设点 ![]() 是直线
是直线 ![]() 上的一动点,过
上的一动点,过 ![]() 点作圆
点作圆 ![]() 的两条切线,切点分别为
的两条切线,切点分别为 ![]() ,求四边形
,求四边形 ![]() 的面积的最小值;
的面积的最小值;
(2)过 ![]() 作直线
作直线 ![]() 的垂线交圆
的垂线交圆 ![]() 于
于 ![]() 点,
点, ![]() 为
为 ![]() 关于
关于 ![]() 轴的对称点,若
轴的对称点,若 ![]() 是圆
是圆 ![]() 上异于
上异于 ![]() 的两个不同点,且满足:
的两个不同点,且满足: ![]() ,试证明直线
,试证明直线 ![]() 的斜率为定值.
的斜率为定值.
【答案】
(1)解:设四边形 ![]() 的面积为
的面积为 ![]() ,
, ![]() ,
,![]() ,所以,当
,所以,当 ![]() 最小时,
最小时, ![]() 就最小,
就最小,![]() ,所以:
,所以: ![]()
(2)解:直线 ![]() 的方程为:
的方程为: ![]() ,代入
,代入 ![]() ,且
,且 ![]() 在第一象限,得
在第一象限,得 ![]() 则
则 ![]() .设
.设 ![]() ,
, ![]() ,
,![]() ,
, ![]() 设直线
设直线 ![]() 的斜率为
的斜率为 ![]() ,则
,则 ![]() 斜率为
斜率为 ![]() ,
,![]() ,
, ![]() ,
,
联立 ![]() 消
消 ![]() 得:
得: ![]() ,
,![]() ,得
,得 ![]() ,
,
同理 ![]() ,
, ,
,
所以,直线 ![]() 的斜率为定值1.
的斜率为定值1.
【解析】(1)首先求出四边形的面积,结合面积以及勾股定理公式得出当 | O P | 最小时, | A P | 就最小,,由题意可知最小距离即为原点到直线l的距离,求出该值即为四边形面积的最小值。(2)首先根据题意由角的相等关系得出直线DM的斜率,再由点斜式求出直线的方程,联立直线与圆的方程消元得到关于x的一元二次方程,结合韦达定理求出xMx1的值,因为xM的值为1进而求出x1的代数式,同理得到x2的代数式,故整理可得直线CD的斜率从而求出其值为1即可。
【考点精析】解答此题的关键在于理解直线的斜率的相关知识,掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?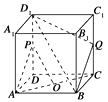
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .将
.将 ![]() 沿
沿 ![]() 折起,使得点
折起,使得点 ![]() 在平面
在平面 ![]() 的正投影
的正投影 ![]() 恰好落在
恰好落在 ![]() 边上,得到几何体
边上,得到几何体 ![]() ,如图2所示.
,如图2所示.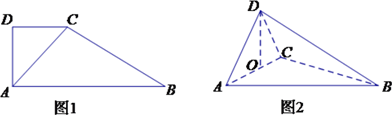
(1)求证: ![]() ;
;
(2)求点 ![]() 到平面
到平面 ![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个正方体的玩具,六个面标注了数字1,2,3,4,5,6,甲、乙两位学生进行如下游戏:甲先抛掷一次,记下正方体朝上的数字 ![]() ,再由乙抛掷一次,记下正方体朝上数字
,再由乙抛掷一次,记下正方体朝上数字 ![]() ,若
,若 ![]() 就称甲、乙两人“默契配合”,则甲、乙两人“默契配合”的概率为( )
就称甲、乙两人“默契配合”,则甲、乙两人“默契配合”的概率为( )
A.![]()
B.![]()
C.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在校学生2 000人,为了学生的“德、智、体”全面发展,学校举行了跑步和登山比赛活动,每人都参加而且只参与其中一项比赛,各年级参与比赛的人数情况如下表:
高一年级 | 高二年级 | 高三年级 | |
跑步人数 | a | b | c |
登山人数 | x | y | z |
其中a∶b∶c=2∶5∶3,全校参与登山的人数占总人数的 ![]() .为了了解学生对本次活动的满意程度,从中抽取一个200人的样本进行调查,则高三年级参与跑步的学生中应抽取( )
.为了了解学生对本次活动的满意程度,从中抽取一个200人的样本进行调查,则高三年级参与跑步的学生中应抽取( )
A.15人
B.30人
C.40人
D.45人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左、右焦点为F1、F2 , 点P是坐标平面内一点,且|OP|=
,其左、右焦点为F1、F2 , 点P是坐标平面内一点,且|OP|= ![]() ,
, ![]()
![]() =
= ![]() ,其中O为坐标原点.
,其中O为坐标原点.
(1)求椭圆C的方程;
(2)如图,过点S(0,﹣ ![]() )的动直线l交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
)的动直线l交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com