
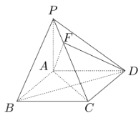
【题目】如图,已知四棱锥![]() 的底面
的底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求三棱锥![]() 的体积
的体积![]() .
.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]()
【解析】
(1)由![]() 平面
平面![]() 得
得![]() ,又底面
,又底面![]() 为菱形可得
为菱形可得![]() ,则
,则![]() 平面
平面![]() ,从而
,从而![]() ;
;
(2)设菱形![]() 的对角线交点为
的对角线交点为![]() ,以
,以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 的方向为
的方向为![]() ,
,![]() 轴建立空间直角坐标系,借助空间向量求出平面法向量的夹角,从而求出答案;
轴建立空间直角坐标系,借助空间向量求出平面法向量的夹角,从而求出答案;
(3)由图可知![]() ,由题意可知三棱锥
,由题意可知三棱锥![]() 的高为
的高为![]() ,由此可求出答案.
,由此可求出答案.
解:(1)因![]() 平面
平面![]() ,故
,故![]() ,
,
又因底面![]() 为菱形,故
为菱形,故![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
∴![]() ;
;
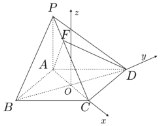
(2)设菱形![]() 的对角线交点为
的对角线交点为![]() ,因
,因![]() ,
,![]() 平面
平面![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 的方向为
的方向为![]() ,
,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴平面![]() 和平面
和平面![]() 的一个法向量分别为
的一个法向量分别为![]() ,
,![]() ,
,
∴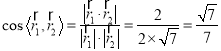 ,
,
由图可知二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)由图可知,![]() ,
,
因![]() ,可知三棱锥
,可知三棱锥![]() 的高为
的高为![]() ,
,
∴![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 和
和![]() 都是定义在
都是定义在![]() 上的单调减函数,且
上的单调减函数,且![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“被追逐函数”,若
上的“被追逐函数”,若![]() ,下述四个结论中正确的是( )
,下述四个结论中正确的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
②若![]() 和函数
和函数![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则
上的“被追逐函数”,则![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”.
上的“被追逐函数”.
A.①③④B.①②④C.②③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
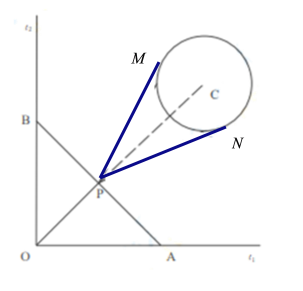
【题目】如图,在一旅游区内原有两条互相垂直且相交于点O的道路l1,l2,一自然景观的边界近似为圆形,其半径约为1千米,景观的中心C到l1,l2的距离相等,点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观,具体方案:在线段OC上取一点P,新建一条道路OP,并过点P新建两条与圆C相切的道路PM,PN(M,N为切点),同时过点P新建一条与OP垂直的道路AB(A,B分别在l1,l2上).为促进沿途旅游经济,新建道路长度之和越大越好,求新建道路长度之和的最大值.(所有道路宽度忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ) 观察3个试验组,用![]() 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com