
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
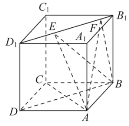
A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着六种不同生肖图案(包含马、羊)的毛绒娃娃各一个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这六个毛绒娃娃中各随机取一个(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达平面
到达平面![]() 外的点
外的点![]() 的位置,
的位置,
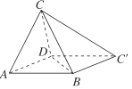
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的外接球的体积;
的外接球的体积;
(3)当![]() 为等腰三角形时,求二面角
为等腰三角形时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,底面ABCD为正方形,![]() 平面CDE.已知
平面CDE.已知![]() ,
,![]() .
.
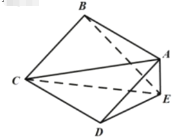
(1)证明:平面![]() 平面ABCD;
平面ABCD;
(2)求直线BE与平面ACE所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 和点
和点![]() ,动点
,动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹曲线
的轨迹曲线![]() 的方程并说明
的方程并说明![]() 是何种曲线;
是何种曲线;
(2)若抛物线![]() :
:![]() 的焦点
的焦点![]() 恰为曲线
恰为曲线![]() 的顶点,过点
的顶点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时.
时.
①求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②定义![]() 其中
其中![]() ,求
,求![]() ;
;
(2)当![]() 时,设
时,设![]() ,
,![]() (
(![]() 为自然对数的底数),若对任意给定的
为自然对数的底数),若对任意给定的![]() ,在
,在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com