
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达平面
到达平面![]() 外的点
外的点![]() 的位置,
的位置,
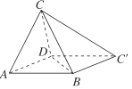
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的外接球的体积;
的外接球的体积;
(3)当![]() 为等腰三角形时,求二面角
为等腰三角形时,求二面角![]() 的大小.
的大小.
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】三角形面积为S=![]() (a+b+c)r,a,b,c为三角形三边长,r为三角形内切圆半径,利用类比推理,可以得出四面体的体积为 ( )
(a+b+c)r,a,b,c为三角形三边长,r为三角形内切圆半径,利用类比推理,可以得出四面体的体积为 ( )
A. V=![]() abc B. V=
abc B. V=![]() Sh
Sh
C. V=![]() (ab+bc+ac)·h(h为四面体的高) D. V=
(ab+bc+ac)·h(h为四面体的高) D. V=![]() (S1+S2+S3+S4)·r(其中S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径,设四面体的内切球的球心为O,则球心O到四个面的距离都是r)
(S1+S2+S3+S4)·r(其中S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径,设四面体的内切球的球心为O,则球心O到四个面的距离都是r)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”.三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的锐角![]() ,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
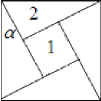
A.30B.40C.50D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的函数f(x)是最小正周期为2π的偶函数,f'(x)是f(x)的导函数,当x∈[0,π]时,0≤f(x)≤1;当x∈(0,π)且x≠![]() 时,
时,![]() ,则函数y=f(x)-|sinx|在区间
,则函数y=f(x)-|sinx|在区间![]() 上的零点个数为( )
上的零点个数为( )
A. 4 B. 6 C. 7 D. 8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
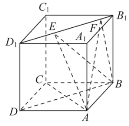
A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,该椭圆的左顶点A到直线
上,该椭圆的左顶点A到直线![]() 的距离为
的距离为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 若线段MN平行于y轴,满足
若线段MN平行于y轴,满足![]() ,动点P在直线
,动点P在直线![]() 上,满足
上,满足![]() 证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正![]() 所在平面垂直平面
所在平面垂直平面![]() ,且边
,且边![]() 在平面
在平面![]() 内,过
内,过![]() 、
、![]() 分别作两个平面
分别作两个平面![]() 、
、![]() (与正
(与正![]() 所在平面不重合),则以下结论错误的是( )
所在平面不重合),则以下结论错误的是( )
A.存在平面![]() 与平面
与平面![]() ,使得它们的交线
,使得它们的交线![]() 和直线
和直线![]() 所成角为
所成角为![]()
B.直线![]() 与平面
与平面![]() 所成的角不大于
所成的角不大于![]()
C.平面![]() 与平面
与平面![]() 所成锐二面角不小于
所成锐二面角不小于![]()
D.平面![]() 与平面
与平面![]() 所成锐二面角不小于
所成锐二面角不小于![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com