
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]()
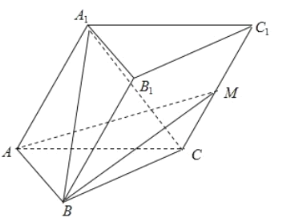
(1)求证:![]() ;
;
(2)若四边形![]() 为正方形,
为正方形,![]() 为正三角形,M是
为正三角形,M是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值
的余弦值
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点为N,通过线线垂直证明
的中点为N,通过线线垂直证明![]() 平面
平面![]() ,即可推出
,即可推出![]() ,利用等腰三角形三线合一的性质即可得证;(2)首先证明
,利用等腰三角形三线合一的性质即可得证;(2)首先证明![]() 为正三棱锥,过点
为正三棱锥,过点![]() 作
作![]() 平面
平面![]() ,则O为正
,则O为正![]() 的中心,取
的中心,取![]() 上靠近点C的三等分点为E,建立空间直角坐标系,利用空间向量法求二面角的余弦值.
上靠近点C的三等分点为E,建立空间直角坐标系,利用空间向量法求二面角的余弦值.
(1)证明:取![]() 的中点为N,在
的中点为N,在![]() 中,
中,![]() ,所以
,所以![]() ,
,

又![]() ,且
,且![]() ,所以
,所以![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以在![]() 中,由
中,由![]() 及
及![]() 的中点为N,得
的中点为N,得![]() .
.
(2)由四边形![]() 为正方形,得
为正方形,得![]() ,
,
由![]() 为正三角形,得
为正三角形,得![]() ,所以
,所以![]()
又由(1)知![]() ,所以
,所以![]() 为正三棱锥,
为正三棱锥,
过点![]() 作
作![]() 平面
平面![]() ,则O为正
,则O为正![]() 的中心,取
的中心,取![]() 上靠近点C的三等分点为E,
上靠近点C的三等分点为E,
则![]() ,
,![]() ,
,![]() 两两垂直,分别以射线
两两垂直,分别以射线![]() ,
,![]() ,
,![]() 为x轴,y轴,z轴的正半轴建立空间直角坐标系,
为x轴,y轴,z轴的正半轴建立空间直角坐标系,
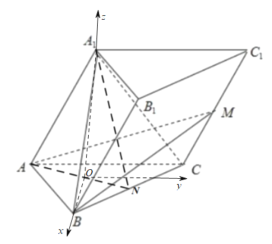
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
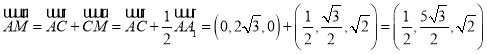 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则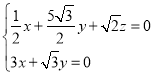 ,取
,取![]() ,得
,得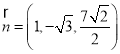 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则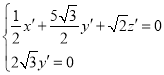 ,所以
,所以![]() ,取
,取![]() ,得
,得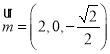
 ,
,
设二面角![]() 为
为![]() ,因为
,因为![]() 为钝角,所以
为钝角,所以![]() ,
,
即所求的二面角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中![]() 表示这些半音的频率,它们满足
表示这些半音的频率,它们满足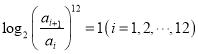 .若某一半音与
.若某一半音与![]() 的频率之比为
的频率之比为![]() ,则该半音为( )
,则该半音为( )
频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
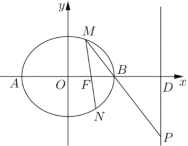
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 的侧棱长都相等,底面
的侧棱长都相等,底面![]() 与侧面
与侧面![]() 都是以
都是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为直线
为直线![]() 上的动点,若平面
上的动点,若平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,则
,则![]() 的最大值是( )
的最大值是( )
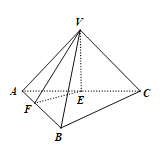
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党的号召,坚决打赢脱贫攻坚战,某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
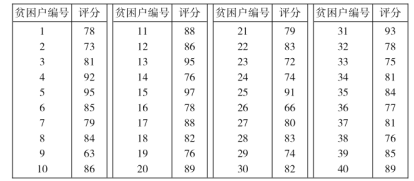
现按贫困户编号从小到大的顺序分组,用系统抽样法从40名贫困户中抽取容量为10的样本.
(1)若在第一分段里随机抽到的第一个样本的评分数据为81,记第二和第十个样本的评分数据分别为a,b,请写出a,b的值;
(2)若10个样本的评分数据分别为92,84,86,78,89,74,83,78,77,89.请你计算所抽到的10个样本的平均数![]() 和方差
和方差![]() ;
;
(3)在(1)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com