
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
【答案】(1)①见解析;②(0,1);(2)证明见解析
【解析】
(1)①对![]() 求导,分别讨论
求导,分别讨论![]() 与
与![]() 的情况即可;
的情况即可;
②由①若![]() 有两个不同的零点,则
有两个不同的零点,则![]() ,由于当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞,则只需使得
,由于当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞,则只需使得![]() 即可,进而求解;
即可,进而求解;
(2)先对![]() 求导,由题可得
求导,由题可得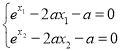 ,两式相减可得
,两式相减可得![]() ,转化
,转化![]() 为
为![]() ,设
,设![]() ,即证
,即证![]() ,进而利用导函数判断单调性证明即可.
,进而利用导函数判断单调性证明即可.
(1)f(x)=h(x)﹣g(x)=ex﹣2x﹣lnx﹣ex+ax2+ax=ax2+(a﹣2)x﹣lnx(x>0),
①![]() (x>0),
(x>0),
(i)当a≤0时,f′(x)<0,函数f(x)在(0,+∞)上递减;
(ii)当a>0时,令f′(x)>0,解得![]() ;令f′(x)<0,解得
;令f′(x)<0,解得![]() ,
,
∴函数f(x)在![]() 递减,在
递减,在![]() 递增;
递增;
综上,当a≤0时,函数f(x)在(0,+∞)上单调递减;
当a>0时,函数f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
②由①知,若a≤0,函数f(x)在(0,+∞)上单调递减,不可能有两个不同的零点,故a>0;
且当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞;
故要使函数f(x)有两个不同的零点,只需![]() ,即
,即![]() ,
,
又函数![]() 在(0,+∞)上为增函数,且
在(0,+∞)上为增函数,且![]() ,故
,故![]() 的解集为(0,1),
的解集为(0,1),
故实数a的取值范围为(0,1)
(2)证明: g′(x)=ex﹣2ax﹣a,依题意,则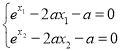 ,两式相减得,
,两式相减得,![]() ,
,
因为a>0,要证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
两边同除以![]() ,即证
,即证![]() ,
,
令t=x1﹣x2(t<0),即证![]() ,
,
令![]() ,则
,则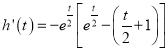 ,
,
令![]() ,则
,则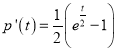 ,
,
当t<0时,p′(t)<0,所以p(t)在(﹣∞,0)上递减,
∴p(t)>p(0)=0,
∴h′(t)<0,
∴h(t)在(﹣∞,0)上递减,
∴h(t)>h(0)=0,即![]() ,
,
故![]() .
.


科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
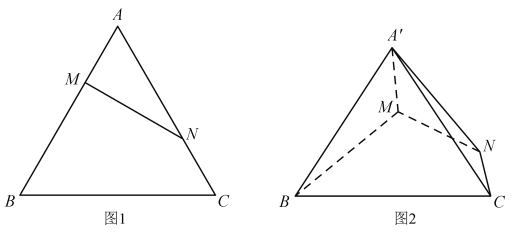
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() 到平面
到平面![]() 的距离为
的距离为![]() .在中任选一个,补充在下面问题的条件中,并作答:
.在中任选一个,补充在下面问题的条件中,并作答:
在线段![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 的体积为
的体积为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
注:如果多个条件分别解答,按第一个解答给分。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐,其中空中梯队编有12个梯队,在领队机梯队、预警指挥机梯队、轰炸机梯队、舰载机梯队、歼击机梯队、陆航突击梯队这6个梯队中,某学校为宣传的需要,要求甲同学需从中选3个梯队了解其组成情况,其中舰载机梯队、歼击机梯队两个梯队中至少选择一个,则不同的选法种数为( )
A.12种B.16种C.18种D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 与焦点在
与焦点在![]() 轴上的椭圆
轴上的椭圆![]() 都过点
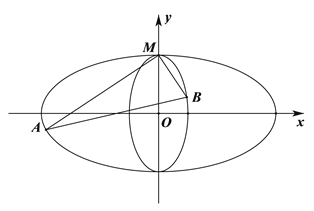
都过点![]() ,中心都在坐标原点,且椭圆
,中心都在坐标原点,且椭圆![]() 与
与![]() 的离心率均为
的离心率均为![]() .
.
(Ⅰ)求椭圆![]() 与椭圆
与椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点M的互相垂直的两直线分别与![]() ,
,![]() 交于点A,B(点A、B不同于点M),当
交于点A,B(点A、B不同于点M),当![]() 的面积取最大值时,求两直线MA,MB斜率的比值.
的面积取最大值时,求两直线MA,MB斜率的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:x﹣y![]() 0将圆O:
0将圆O:![]() 分成的两部分的面积之比为( )
分成的两部分的面积之比为( )
A.(4π![]() ):(8π
):(8π![]() )B.(4π﹣3
)B.(4π﹣3![]() ):(8π+3
):(8π+3![]() )
)
C.(2π﹣2![]() ):(10π+2
):(10π+2![]() )D.(2π﹣3
)D.(2π﹣3![]() ):(10π+3
):(10π+3![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
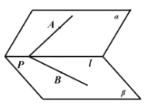
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com