
【题目】直线l:x﹣y![]() 0将圆O:
0将圆O:![]() 分成的两部分的面积之比为( )
分成的两部分的面积之比为( )
A.(4π![]() ):(8π
):(8π![]() )B.(4π﹣3
)B.(4π﹣3![]() ):(8π+3
):(8π+3![]() )
)
C.(2π﹣2![]() ):(10π+2
):(10π+2![]() )D.(2π﹣3
)D.(2π﹣3![]() ):(10π+3
):(10π+3![]() )
)
【答案】B
【解析】
根据题意,设直线l与圆O:x2+y2=4交于点MN,过点O作OP⊥MN,垂足为点P,求出|OP|的值,结合直线与圆的位置关系可得∠MON![]() 以及|MN|=2
以及|MN|=2![]() ;进而计算可得S△MON和S扇形OMN的值,据此可得直线l将圆O分成的两部分的面积,计算即可得答案.
;进而计算可得S△MON和S扇形OMN的值,据此可得直线l将圆O分成的两部分的面积,计算即可得答案.
解:根据题意,设直线l与圆O:x2+y2=4交于点MN,过点O作OP⊥MN,垂足为点P,
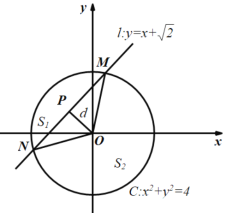
则点O到直线l的距离|OP|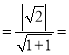 1,
1,
又由圆O:x2+y2=4的半径|OM|=r=2,则∠MOP![]() ,则∠MON
,则∠MON![]() ;
;
同时|MP|![]() ,则|MN|=2
,则|MN|=2![]() ,
,
且S△MON![]() |OP|×|MN|
|OP|×|MN|![]() ,
,
则S扇形OMN![]() r2
r2![]() ,
,
则劣弧对应的弓形的面积S1![]() ,
,
另一部分的面积S2=πr2﹣S1=4π﹣(![]() )
)![]() ,
,
故两部分的面积之比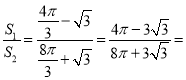 (4π﹣3
(4π﹣3![]() ):(8π+3
):(8π+3![]() ).
).
故选:B.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
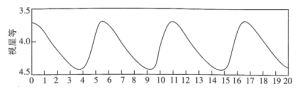
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国经济取得了长足的进步,同时性别比例问题日益突出.根据国家统计局发布的2019年统计年鉴,将国家31个省级行政区(特别行政区未记人)的人均国内生产总值与人口性别比例(每100位女性所对应的男性数目)做出了如下柱状图.从人口统计学角度来说,性别比例正常范围在102至107之间.人均国内生产总值小于6.5万元人民币(约1万美元)称为欠发达地区,大于或等于6.5万元的地区称为发达地区.
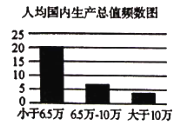
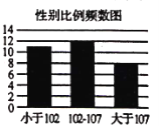
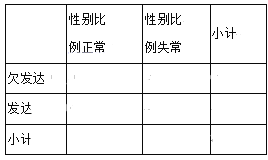
(1)已知性别比例正常的省级行政区中欠发达的行政区的个数是发达行政区的两倍,完成列联表,并判断是否有90%的把握认为各省级行政区的性别比例与经济发展程度有关;
(2)在人均国内生产总值介于6.5万与10万之间的7省级行政区中,有3个人口性别比例正常,从中任取两个,求抽到两个省级行政区的人口性别比例都正常的概率.
附:参考公式及临界值表
 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A. B.
B.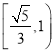
C.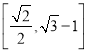 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】F是抛物线![]() 的焦点,M是抛物线C上位于第一象限内的任意一点,过
的焦点,M是抛物线C上位于第一象限内的任意一点,过![]() 三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
三点的圆的圆心为Q,点Q到抛物线C的准线的距离为![]() .
.
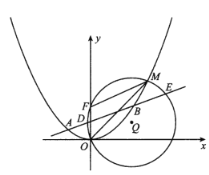
(1)求抛物线C的方程;
(2)若点M的横坐标为![]() ,直线
,直线![]() 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点(
为抛物线上一点(![]() 在
在![]() 轴上方),
轴上方),![]() ,
,![]() 点到
点到![]() 轴的距离为4.
轴的距离为4.
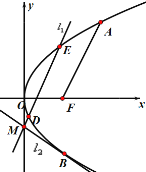
(1)求抛物线方程及点![]() 的坐标;
的坐标;
(2)是否存在![]() 轴上的一个点
轴上的一个点![]() ,过点
,过点![]() 有两条直线
有两条直线![]() ,满足
,满足![]() ,
,![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.![]() 与抛物线相切于点
与抛物线相切于点![]() (
(![]() 不为坐标原点),有
不为坐标原点),有![]() 成立,若存在,求出点
成立,若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为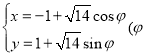 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 的交线为直线
的交线为直线![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求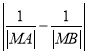 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com