
【题目】已知函数![]() ,集合
,集合![]() .
.
(1)若集合![]() 中有且仅有
中有且仅有![]() 个整数,求实数
个整数,求实数![]() 的取值范围;
的取值范围;
(2)集合![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将函数解析式变形为![]() ,根据对称性可知集合
,根据对称性可知集合![]() 中的
中的![]() 个整数只能是
个整数只能是![]() 、
、![]() 、
、![]() ,然后对
,然后对![]() 与
与![]() 的大小进行分类讨论,结合题意可得出实数
的大小进行分类讨论,结合题意可得出实数![]() 的取值范围;
的取值范围;
(2)对![]() 与
与![]() 的大小进行分类讨论,结合
的大小进行分类讨论,结合![]() 可得出
可得出![]() 所满足的不等式,结合
所满足的不等式,结合![]() 的取值范围,可求得实数
的取值范围,可求得实数![]() 的取值范围.
的取值范围.
(1)![]() .
.
因为集合![]() 中有且仅有
中有且仅有![]() 个整数,则
个整数,则![]() ,即
,即![]() .
.
①若![]() ,即当
,即当![]() 时,
时,![]() ,
,
由于![]() 与
与![]() 的平均数为
的平均数为![]() ,则
,则![]() ,则
,则![]() 中的
中的![]() 个整数只可能是
个整数只可能是![]() 、
、![]() 、
、![]() ,
,![]() ;
;
②![]() ,即当
,即当![]() 时,
时,![]() ,
,
由于![]() 与
与![]() 的平均数为
的平均数为![]() ,则
,则![]() ,则
,则![]() 中的
中的![]() 个整数只可能是
个整数只可能是![]() 、
、![]() 、
、![]() ,
,![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)①若![]() ,即
,即![]() 时,则
时,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得![]() ;
;
②当![]() 时,即当
时,即当![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,则
,则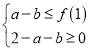 ,得
,得![]() ,
,
![]() ,可得
,可得![]() ,
,![]() ,
,
![]() ,
,![]() ,此时
,此时![]() ;
;
③若![]() ,即当
,即当![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,则
,则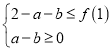 ,得
,得![]() ,
,
所以![]() ,则
,则![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
![]() ,
,![]() ,此时
,此时![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意![]()
![]()
![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有
上恰有![]() 个零点.
个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.
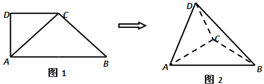
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,E,F是AD,BD中点,![]() ,
,![]() ,将
,将![]() 沿对角线BD折起至
沿对角线BD折起至![]() ,使平面
,使平面![]() 平面BCD,则四面体
平面BCD,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
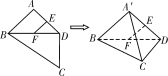
A.![]() 平面
平面![]()
B.异面直线CD与![]() 所成的角为
所成的角为![]()
C.异面直线EF与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面BCD所成的角为
与平面BCD所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
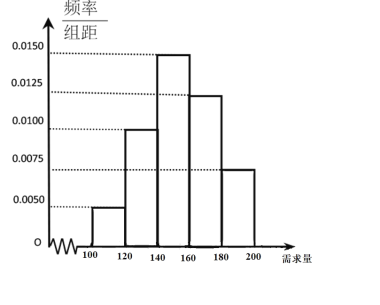
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数和众数;
的平均数和众数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)以需求量的频率作为各需求量的概率,求开学季利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,给出下述四个结论:
,给出下述四个结论:
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②将函数![]() 的图象向左平移
的图象向左平移![]() 所得图象关于原点对称;
所得图象关于原点对称;
③函数![]() 在区间
在区间![]() ,上单调递增;
,上单调递增;
④函数![]() 在区间
在区间![]() 上有
上有![]() 个零点.
个零点.
其中所有正确结论的编号是( )
A.①②B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x+1).
(1)若0<f(1-2x)-f(x)<1,求实数x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),当x∈[1,2]时,求函数y=g(x)的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com