
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②比较![]() 与
与![]() 的大小;
的大小;
(2)当![]() 时,若对
时,若对![]() 时,
时,![]() ,且
,且![]() 有唯一零点,证明:
有唯一零点,证明:![]() .
.
【答案】(1)①见解析,②见解析;(2)见解析
【解析】
(1)①把![]() 代入函数解析式,求出函数的导函数得到
代入函数解析式,求出函数的导函数得到![]() ,再求出
,再求出![]() ,利用直线方程的点斜式求函数
,利用直线方程的点斜式求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②令![]() ,利用导数研究函数的单调性,可得当
,利用导数研究函数的单调性,可得当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)由题意,![]() ,
,![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .利用导数可得当
.利用导数可得当![]() 时,
时,![]() 在
在![]() 上单调递减,当
上单调递减,当![]() ,
,![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,得到
上单调递增,得到![]() .由
.由![]() 在
在![]() 恒成立,且
恒成立,且![]() 有唯一解,可得
有唯一解,可得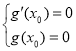 ,得
,得![]() ,即
,即![]() .令
.令![]() ,则
,则![]() ,再由
,再由![]() 在
在![]() 上恒成立,得
上恒成立,得![]() 在
在![]() 上单调递减,进一步得到
上单调递减,进一步得到![]() 在
在![]() 上单调递增,由此可得
上单调递增,由此可得![]() .
.
解:(1)①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 切线方程为
切线方程为![]() ,即
,即![]() ;
;
②令![]() ,
,
则![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
证明:(2)由题意,![]() ,
,
而![]() ,
,
令![]() ,解得
,解得![]() .
.
![]() ,
,![]()
![]() ,
,
![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() ,
,![]() 时,
时,![]() ,
,![]() 在
在![]() ,
,![]() 上单调递增.
上单调递增.
![]() .
.
![]() 在
在![]() 恒成立,且
恒成立,且![]() 有唯一解,
有唯一解,
![]()
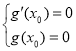 ,即
,即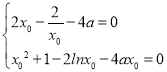 ,
,
消去![]() ,得
,得![]() ,
,
即![]() .
.
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
, ![]() ,
,
![]() .
.
![]() 在
在![]() 上单调递增,
上单调递增,
![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
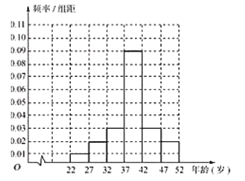
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
|
|
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年9月支付宝宣布在肯德基的KPRO餐厅上线刷脸支付,也即用户可以不用手机,单单通过刷脸就可以完成支付宝支付,这也是刷脸支付在全球范围内的首次商用试点.某市随机抽查了每月用支付宝消费金额不超过3000元的男女顾客各300人,调查了他们的支付宝使用情况,得到如下频率分布直方图:
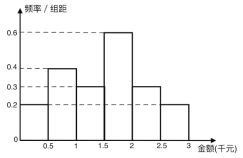
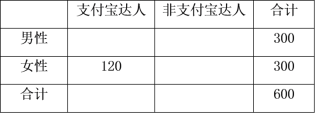
若每月利用支付宝支付金额超过2千元的顾客被称为“支付宝达人”, 利用支付宝支付金额不超过2千元的顾客称为“非支付宝达人”.
(I)若抽取的“支付宝达人”中女性占120人,请根据条件完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
(II)支付宝公司为了进一步了解这600人的支付宝使用体验情况和建议,从“非支付宝达人” “支付宝达人”中用分层抽样的方法抽取8人.若需从这8人中随机选取2人进行问卷调查,求至少有1人是“支付宝达人”的概率.
附:参考公式与参考数据如下
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“速增函数”.
为“速增函数”.
(1)试判断函数![]() 与
与![]() 是否是“速增函数”;
是否是“速增函数”;
(2)若函数![]() 为“速增函数”,求
为“速增函数”,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“速增函数”,且
为“速增函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
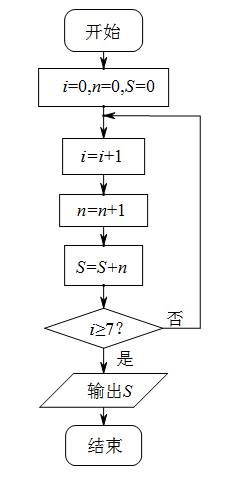
A.28B.56C.84D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com