
【题目】已知函数![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)讨论![]() 的导函数
的导函数![]() 的零点的个数;
的零点的个数;
(2)若![]() ,且
,且![]() 在
在![]() 上的最小值为
上的最小值为![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
【答案】(1)当![]() 时,
时,![]() 存在唯一零点,当
存在唯一零点,当![]() 时,
时,![]() 无零点.(2)证明见解析
无零点.(2)证明见解析
【解析】
(1)由题意得![]() 的定义域为
的定义域为![]() ,
,![]() ,然后分
,然后分![]() 和
和![]() 两种情况讨论即可
两种情况讨论即可
(2)先由条件求出![]() ,然后要证
,然后要证![]() ,即证
,即证![]() ,令
,令![]() ,然后利用导数得出
,然后利用导数得出![]() 即可
即可
(1)由题意,得![]() 的定义域为
的定义域为![]() ,
,![]() .
.
显然当![]() 时,
时,![]() 恒成立,
恒成立,![]() 无零点.
无零点.
当![]() 时,取
时,取![]() ,
,
则![]() ,即
,即![]() 单调递增,
单调递增,
又![]() ,
,![]() ,
,
所以导函数![]() 存在唯一零点.
存在唯一零点.
故当![]() 时,
时,![]() 存在唯一零点,当
存在唯一零点,当![]() 时,
时,![]() 无零点.
无零点.
(2)由(1)知,当![]() 时,
时,![]() 单调递增,所以
单调递增,所以![]() ,所以
,所以![]() .
.
因为![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
根据题意,要证![]() ,即证
,即证![]() ,只需证
,只需证![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
所以![]() 有唯一的零点
有唯一的零点![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增,
单调递增,
所以![]() .
.
又因为![]() ,所以
,所以![]() ,所以
,所以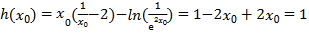 ,
,
故![]() .
.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x2+ax+lnx(a∈R)
x2+ax+lnx(a∈R)
(1)讨论函数f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2且|x1﹣x2|![]() ,求|f(x1)﹣f(x2)|的最大值.
,求|f(x1)﹣f(x2)|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某流行病爆发期间,某市卫生防疫部门给出的治疗方案中推荐了三种治疗药物![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
|
|
|
|
单价(单位:元) | 600 | 1000 | 800 |
治愈率 |
|
|
|
市场使用量(单位:人) | 305 | 122 | 183 |
(Ⅰ)从感染患者中任取一人,试求其一个疗程被治愈的概率大约是多少?
(Ⅱ)试估算每名感染患者在一个疗程的药物治疗费用平均是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
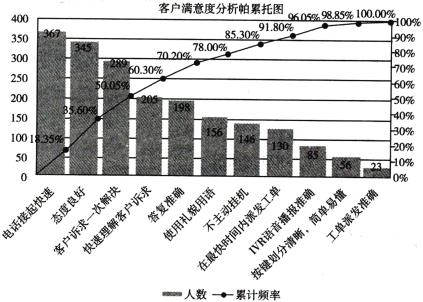
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.

(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3.
(1)求椭圆C的标准方程;
(2)过点P(0,1)的直线l与椭圆C交于两点A,B.己知在椭圆C上存在点Q,使得四边形OAQB是平行四边形,求Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为
的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为![]() 和
和![]() .
.
(1)求![]() 的值;
的值;
(2)![]() ,
,![]() ,求四边形PAEG面积的最小值.
,求四边形PAEG面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com