
 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由;
的大小关系,并说明理由; (n∈N*).
(n∈N*). (x>1)利用志数证明得函数在(1,+∞)上单调递增,由x1<x2<x3得y1<y2<y3,则
(x>1)利用志数证明得函数在(1,+∞)上单调递增,由x1<x2<x3得y1<y2<y3,则 =(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,则B是钝角,最后结合余弦定理和正弦定理得sin2A+sin2C<sin2B.从而得到证明;
=(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,则B是钝角,最后结合余弦定理和正弦定理得sin2A+sin2C<sin2B.从而得到证明; x∈[1,+∞),由(Ⅰ)得g(x)是[1,+∞)上的减函数,将区间[1,n](n>1)n-1等分,由定积分定义及几何意义得到证明.
x∈[1,+∞),由(Ⅰ)得g(x)是[1,+∞)上的减函数,将区间[1,n](n>1)n-1等分,由定积分定义及几何意义得到证明. ,由题意得
,由题意得 ,
, 得f(x)在(-∞,-1),(1,+∞)上是减函数,在(-1,1)上是增函数,故f(x)的极小值=
得f(x)在(-∞,-1),(1,+∞)上是减函数,在(-1,1)上是增函数,故f(x)的极小值= ,f(x)的极大值=
,f(x)的极大值= …(4分)
…(4分) (x>1)y'=
(x>1)y'= ,函数在(1,+∞)上单调递增,由x1<x2<x3得y1<y2<y3…(6分)
,函数在(1,+∞)上单调递增,由x1<x2<x3得y1<y2<y3…(6分) =(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,则B是钝角
=(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,则B是钝角 ,即a2+c2<b2,
,即a2+c2<b2, >
> >1,
>1, >
> …(9分)
…(9分) x∈[1,+∞),由(Ⅰ)得g(x)是[1,+∞)上的减函数,
x∈[1,+∞),由(Ⅰ)得g(x)是[1,+∞)上的减函数,
 …(14分)
…(14分)

科目:高中数学 来源: 题型:解答题
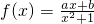 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0.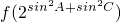 与
与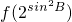 的大小关系,并说明理由.
的大小关系,并说明理由.查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省龙岩市武平一中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.查看答案和解析>>
科目:高中数学 来源:福建省月考题 题型:解答题
 图象在x=1处的切线方程为2y﹣1=0.
图象在x=1处的切线方程为2y﹣1=0. 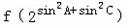 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com