
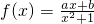 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0.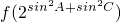 与
与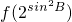 的大小关系,并说明理由.
的大小关系,并说明理由.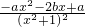 ,
, ,
,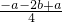 =0,
=0, =
= ,
,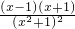 >0,解得:x<-1或x>1;
>0,解得:x<-1或x>1;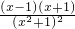 <0,解得:-1<x<1,
<0,解得:-1<x<1, ,f(x)的极大值为f(1)=
,f(x)的极大值为f(1)= ;…(6分)
;…(6分) +ln(x-1)(x>1),
+ln(x-1)(x>1),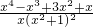 >0,
>0, •
• =(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,
=(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0, <0,即a2+c2<b2,
<0,即a2+c2<b2,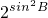 >
>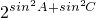 >1,
>1,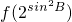 >
>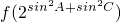 .…(14分)
.…(14分) ,列出两个关于a与b的方程,联立求出a与b的值,代入确定出导函数解析式,根据导函数值的正负得到函数的增减性,根据增减性得到函数的极小值及极大值即可;
,列出两个关于a与b的方程,联立求出a与b的值,代入确定出导函数解析式,根据导函数值的正负得到函数的增减性,根据增减性得到函数的极小值及极大值即可; •
• ,得到其值小于0,可得出B为钝角,利用余弦定理表示出cosB,根据B为钝角可得出cosB小于0,整理后得到a2+c2<b2,再利用正弦定理化简得到sin2A+sin2C<sin2B,根据f(x)是(1,+∞)上的增函数,可得出
,得到其值小于0,可得出B为钝角,利用余弦定理表示出cosB,根据B为钝角可得出cosB小于0,整理后得到a2+c2<b2,再利用正弦定理化简得到sin2A+sin2C<sin2B,根据f(x)是(1,+∞)上的增函数,可得出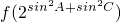 与
与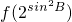 的大小关系.
的大小关系.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:2011-2012学年福建省龙岩市武平一中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.查看答案和解析>>
科目:高中数学 来源:福建省月考题 题型:解答题
 图象在x=1处的切线方程为2y﹣1=0.
图象在x=1处的切线方程为2y﹣1=0. 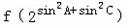 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.查看答案和解析>>
科目:高中数学 来源:2011年福建省南平市高三适应性考试数学试卷(理科)(解析版) 题型:解答题
 图象在x=1处的切线方程为2y-1=0.
图象在x=1处的切线方程为2y-1=0. 与
与 的大小关系,并说明理由;
的大小关系,并说明理由; (n∈N*).
(n∈N*).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com